2004.4.28
化学工学トップページ >
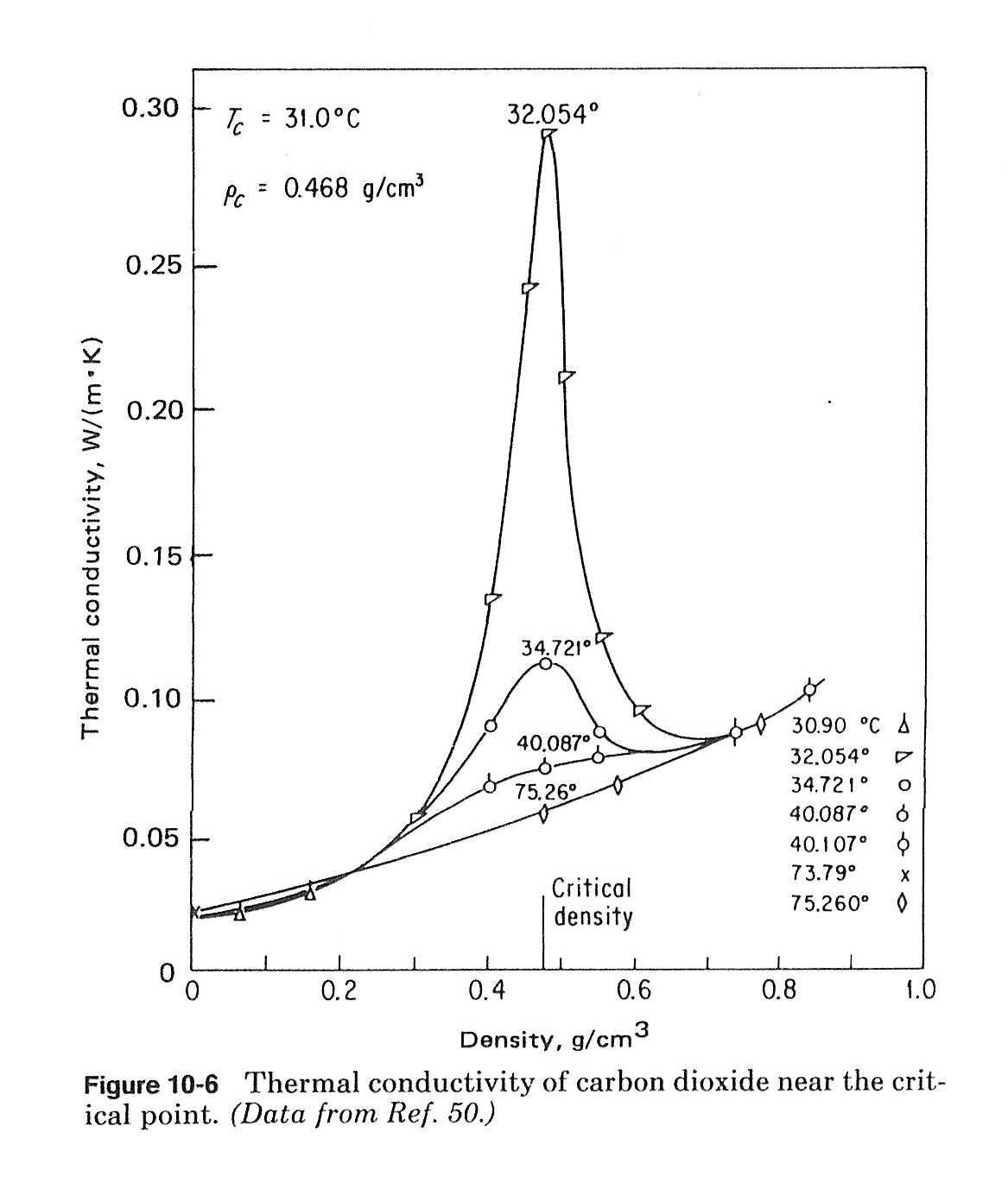
データソースはこれ。
Gas&Liquidからとってきました。
二酸化炭素の熱伝導率は臨界点近傍で急に大きくなります。
これは臨界発散と呼ばれる現象です。
気体の熱伝導率は液体の熱伝導率の1/10ぐらいになってしまいます。
それは気体がすかすかで熱の高い(運動エネルギーの高い)分子が他の分子にぶつかってエネルギーのやり取りをする確率が低いからです。
それでは超臨界状態では何故液体よりさらに熱伝導率が高くなるのかと言うとビリヤードみたいなものと説明されています。
ビリヤードで最初にブレークする時には一つのボールを強く突きます。
(熱の高い分子)それが十分長い距離走って10個のボールの固まりにぶつかるとエネルギーの授受が行われ10個は弾け飛びます。
(熱の高い分子から熱伝導して高い熱になった)これがボールがうじゃうじゃいる所でボールを強く突くと他のボールにはスピードが伝わらず弾き上がってしまいます。
(気体になってしまう)そんなわけで臨界点近傍では熱伝導率は非常に高くなるらしいです。
(自分はあまり詳しく無いのでもし説明が間違っていたらごめんなさい。専門家の御指摘をお待ちしています。)
詳しくは豊田中央研究所の福嶋喜章博士の研究を参照してください。
引用させて頂くと「全体が均一な溶液系でありながら、分子の周囲の状況が常に変化し大きなゆらぎを実現している不均一な状態も同時に実現しているのが超臨界流体の特徴である。このような「ゆらぎ」により、液体と気体の長所を同時に実現出来る溶媒と言える」 といっている。
この超臨界密度のグラフを見て頂くと判る通り、横軸は二酸化炭素の密度になっています。
しかし実際に観測できる値は温度と圧力です。
あるタンクにポンプで二酸化炭素を入れて行く。
タンクには温度計と圧力計が付いている。
タンクの容量と何グラム二酸化炭素を入れたかで密度は計算できます。
しかしその中で重合を行おうとした場合、(超臨界重合)重合熱で温度は変わる、
圧力は変わる原料のフィードと抜き出しで密度はいくつになっているのかわからないって言う事が多くなってしまいます。
そこで密度の推算アプレットが大事になります。
これを使えば任意での温度と圧力から密度は計算できます。
それでは今月のテーマ、温度と密度から熱伝導率を推算するアプレットを作成します。密度の時と同様に図中のデータポイントを読み取ります。
name ThC Density Temperature
1 0.020348 0.068477 32.054
2 0.025187 0.156613 32.054
3 0.037521 0.241602 32.054
4 0.052397 0.300537 32.054
5 0.083498 0.361349 32.054
6 0.130027 0.402827 32.054
7 0.186981 0.431417 32.054
8 0.239376 0.450154 32.054
9 0.269316 0.460394 32.054
10 0.276803 0.462139 32.054
11 0.283449 0.468763 32.054
12 0.288023 0.470464 32.054
13 0.292172 0.47705 32.054
14 0.288416 0.483516 32.054
15 0.284668 0.48509 32.054
16 0.280089 0.486651 32.054
17 0.273013 0.488174 32.054
18 0.265931 0.492958 32.054
19 0.237626 0.499051 32.054
20 0.208079 0.501863 32.054
21 0.182687 0.507999 32.054
22 0.158534 0.519047 32.054
23 0.136456 0.533388 32.054
24 0.115199 0.554265 32.054
25 0.097245 0.589869 32.054
26 0.084273 0.632072 32.054
27 0.080839 0.692359 32.054
28 0.082831 0.742944 32.054
29 0.097217 0.844272 32.054
30 0.019935 0.06684 34.721
31 0.025187 0.156613 34.721
32 0.037518 0.243233 34.721
33 0.051559 0.303785 34.721
34 0.065207 0.351286 34.721
35 0.084669 0.405398 34.721
36 0.097935 0.433324 34.721
37 0.10166 0.444796 34.721
38 0.104544 0.461148 34.721
39 0.10659 0.480748 34.721
40 0.105313 0.497037 34.721
41 0.101959 0.511663 34.721
42 0.094863 0.524601 34.721
43 0.083164 0.552147 34.721
44 0.078114 0.584685 34.721
45 0.075136 0.622148 34.721
46 0.076701 0.67925 34.721
47 0.083244 0.744581 34.721
48 0.096801 0.844265 34.721
49 0.019519 0.066833 40.087
50 0.025184 0.158244 40.087
51 0.037102 0.243226 40.087
52 0.04906 0.305378 40.087
53 0.059767 0.369142 40.087
54 0.063455 0.401814 40.087
55 0.066316 0.431212 40.087
56 0.068761 0.460603 40.087
57 0.07079 0.489988 40.087
58 0.07199 0.51773 40.087
59 0.073176 0.553625 40.087
60 0.074358 0.591151 40.087
61 0.075524 0.638462 40.087
62 0.076282 0.680874 40.087
63 0.082831 0.742944 40.087
64 0.097217 0.844272 40.087
65 0.023688 0.062004 75.26
66 0.030576 0.168111 75.26
67 0.035435 0.244832 75.26
68 0.043985 0.352594 75.26
69 0.047638 0.404835 75.26
70 0.05008 0.435857 75.26
71 0.05376 0.473421 75.26
72 0.058262 0.51589 75.26
73 0.061104 0.556703 75.26
74 0.07014 0.623703 75.26
75 0.07545 0.680861 75.26
76 0.082415 0.742937 75.26
77 0.097214 0.845902 75.26これをニューラルネットワークに学習させ任意の温度と密度の時の熱伝導率を予測する推算式を作ります。超臨界CO2の密度の推算の時も、フルゾーンの撹拌翼の動力計算の時も図を読み取ってニューラルネットワークで学習させるという方法をとりました。
ニューラルネットワークには実は非常に大きな欠点があります。
それは外挿性の欠如と言う問題です。
ニューラルネットワークは学習した範囲については正しい答えを出せますが学習した範囲外では非常に変な答えをかえします。
非線形性を取り込んでしまうのでそのはずれ方は目をおおうばかりになります。
ところがこうした図を読み取って学習させる場合、例えば密度では温度は40-120度の範囲で計算できれば良い。
圧力も0-400barの間だけでよい。
つまり外挿性の欠如と言う問題を考える必要が無い。撹拌翼の場合も、フルゾーンとアンカー翼の中間の翼などないのでレイノルズ数だけの依存性で良く、しかもそのRe数に関しても上限と下限を外れた所を推算する必要は全く無い。
従ってこうしたものをニューラルネットワークで学習させるのは非常にいいテーマだと言えます。
非線形性があってしかも内挿だけでよい。
そこで今回の熱伝導率も楽勝だと思って始めたのですがこれが難しい事難しい事。
もしニューラルネットワークの専門家がこのページを見たら是非チャレンジしてみて下さい。
テーマとしては非常にいいテーマのはずがなんでこんなに難しいのか一緒に議論したいと思います。
作り上げるのにゆうに2ヶ月はかかってしまいました。まだ不満はありますが一応の結果がでたのでUPします。
要望が多ければ、HTML5のプログラムに書き直します。
古いJAVAの記述
二酸化炭素の熱伝導率推算JAVAアプレット
使い方は簡単です。温度を指定してCalcボタンを押して下さい。圧力を自動的に変え密度を推算し、その密度と温度から熱伝導率を推算します。ラジオボタンで密度を選ぶと圧力をスキャンしながら密度を推算します。
ブラウザーがJAVAをサポートしていて、運良く古いJAVAが走れば、以下のような画面が出てくる。温度を入れてCalcボタンを押すと熱伝導率を密度に対してプロットする。テキストエリアのデータはコピーして表計算ソフトに持って行って使える。
2012.1.10
JAVAのコピー&ペーストができないという問題が指摘された。これはjava.policyを書き換えればいいそうだ。Windowsを使っているなら、こちらの記事を参照してください。
Macでは、ライブラリー/JAVA/HOMEに行き、そこのsecurityのフォルダーのオーナーに自分を入れて、その中のjava.policyを書き換える。詳しくはこちらの記事を参照(英語)。
grant { permission java.awt.AWTPermission "accessClipboard"; };
自分は全部書き換えてしまった。(自己責任でやってください!)
2013.2.9 MacでもJava PolicyToolが使えるそうだ。自分のホームディレクトリーに.java.policyを書き込めばシステムのSeculityをいじらなくても変更できる。SafariはローカルのJava Appletを走らせる事ができなくなった。MacのWeb共有を立ち上げて、ライブラリー/WebServer/Documents/にプログラムを置き、http://localhost/から呼び出せば良い。localhostではなくhttp://10.0.1.2/などと入れてしまいお気に入りに登録してしまうと、立ち上げ直した時などに番号が変わる事があり呼び出せなくなる
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
