2025.05.15
pirika.comで化学 > 化学全般
> 次世代HSP2, Pirika Pro for MI >あなたは、酸? 塩基?
> ハンセン溶解度パラメータ (HSP) Doc
注意:HSPiPの機能ではありません
あなたは、酸? 塩基? 挟み撃ち法の限界?

なんだか分からないけど白い粉がある。でも、酸性か塩基性かのどちらかだとわかっている。右手でない方の手が左手という定義が意味ないように、(異性にモテるなんていう用語も”不適切にも程がある”けど)どのような溶媒に好かれたら酸で、逆には塩基なのだろうか?
なんで、モテるなんていう用語を危険を覚悟で使っているかというと、HSPの基本概念で, Likes dissolve Likesというのがある。この場合のLikesは”似たもの”という意味だが、普通の”Like=好き”でダジャレているだけだ。AIですら理解してこの絵を描いてくれた。
オレイン酸の溶解度
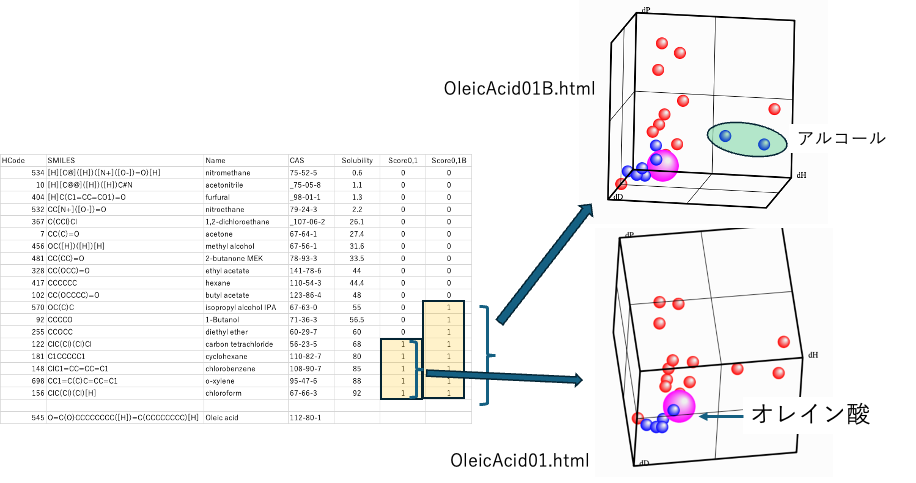
オレイン酸の溶解度のデータが(確か)油脂なんとかハンドブックにあった。
普通の定性的なHSPを調べるなら、溶解度の適当な値で区切って、ある値以上を良溶媒(Score 1), 貧溶媒(Score 0)として、Sphere用のデータを作る。作成方法は色々な所で書いているので、ここでは省略する。YMB25Proを使えば簡単にデータ作成できる。
まずは、よく溶ける5つをScore 1にした場合。
この5つの溶媒はClassicな3Dの位置で似通った位置にある。
ところがアルコールなどを3つ加えると大きく様相が変わる。
実際に回転させてみてみれば簡単にわかるが、アルコールまでScore 1に含めるとマゼンタ色のオレイン酸から遠く離れた。IPA, n-ブタノールが良溶媒になる。
アルコールまで含めたハンセンの溶解球を求めようとすると、逆に貧溶媒が溶解球の中に入ってきてしまう。そこで、よく溶けるもの5つを良溶媒に設定する。
Sphere法の原理
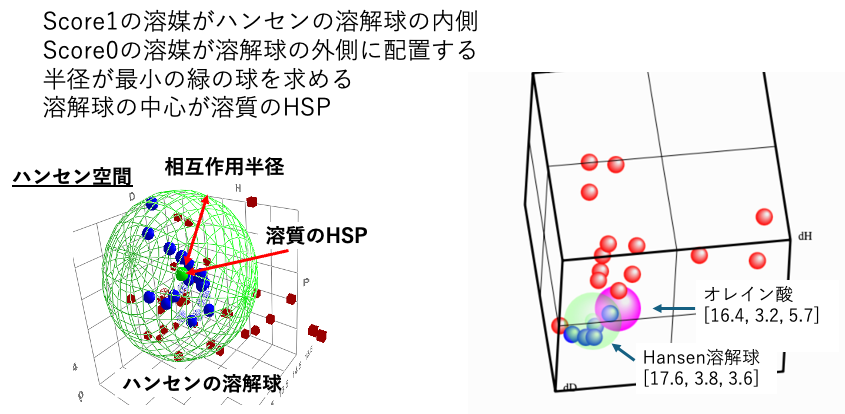
Hansen先生が確立されたSphere法というのは、Score1の溶媒がハンセンの溶解球の内側に配置され、Score0の溶媒が溶解球の外側に配置される。半径が最小の緑の球を求めることだ。溶解球の中心が溶質のHSPとなる。
Hansen溶解球の中心は[17.6, 3.8, 3.6]、半径は2.51となる。間違って認識される溶媒は無い。
溶質の酸塩基に関してはわからない
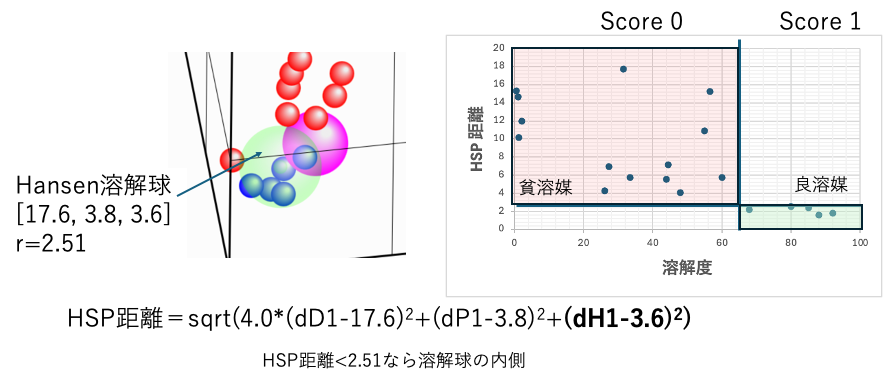
dD項の差分の前に4.0というファクターがついていることに注意しよう。
次世代のHSP2で扱う、dDを分割した式では4.0はいらなくなるが、ClassicなHSPではこの4.0が必要になる。
ここに示したように、Score 0,1で計算を行った場合には、定性的なSphereを求めたことになる。良溶媒(貧溶媒)の溶解量とHSP距離には相関がない。同じHSP距離でも異なる溶解量の溶媒が多数存在する。
右の図で、もう一つ、ジエチルエーテルが良溶媒と設定したとしよう。
すると、さらに2つ以上、貧溶媒なのにHSP距離が短いものが現れてしまう。
3D座標を良く見ながら、Scoreを決めていく必要がある。
HSP: 基本原理
HSPの基本原理は、HSP距離が短ければ、より良く溶解するだ。
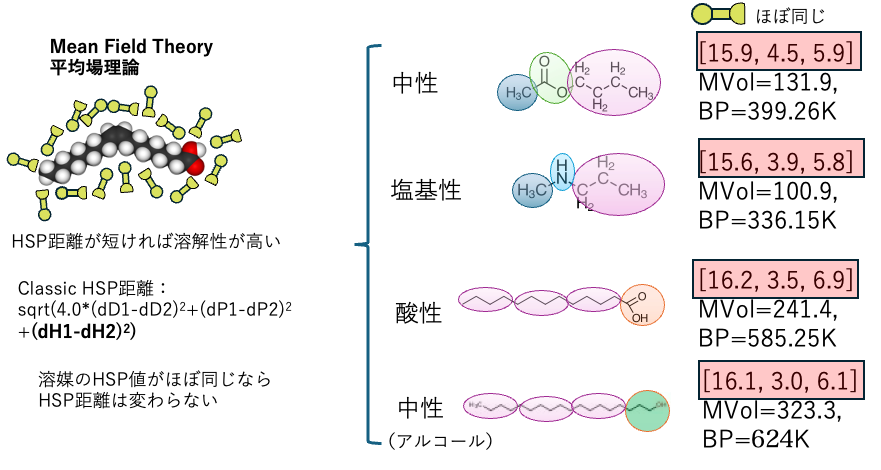
そして分子のSP値の総量、tot HSPは
tot HSP = ((Hv -RT)/MVol)0.5
とMVol,分子体積で規格化される。そこでアルコールやカルボキシル基を持っていて蒸発潜熱(Hv)が大きくても、分子体積が大きければHSPは小さくなる。
そこで、図中の4つの化合物のHSPはほぼ同じになる。
HSPの基本原理から言うと、ここにある4つの化合物はどんな溶質であってもHSP距離が同じなので同じ溶解性になる。
それがClassicなHSPの原理になる。
無機物の分散などを行っている研究者は、すぐにおかしいと感じるかもしれないが、普通のポリマーの溶解では、50年以上この考え方は支持されてきた。
δHの酸、塩基性分割
Hansen先生とHSPを開発している私やAbbott先生は、dH項の分割に取り組んできた。
ロンドン大学のAbraham教授から化合物のAcid/Baseの値を頂き、HSPiPに搭載してきた。

HSPiPを用いたdHAcid,dHBase解析
HSPiPでdHのAcid/Baseの分割を用いる場合には、dHD/Aまで含めたデータを用意しなければならない。Pirika25Pro4MIのユーザーはCAS番号から、もしくはSMILESの構造式から簡単に作ることができる。
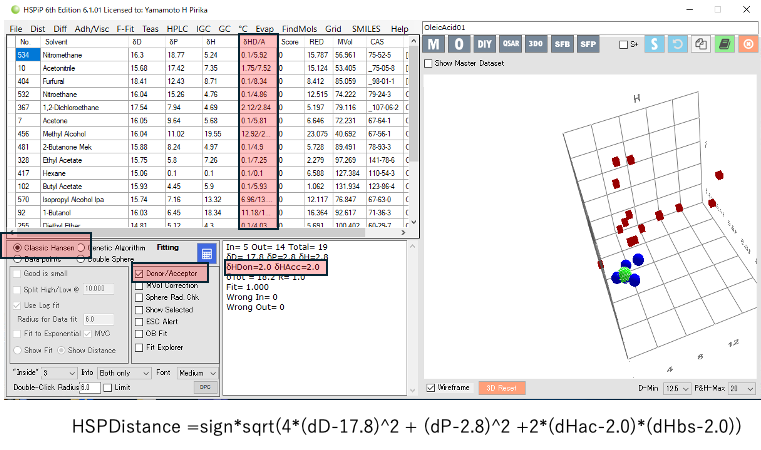
データを読み込んだ後、Classic Hansenを選択すると(GA, Double Sphere, Data Pointでは選べない) Donor/Acceptorが選択できる。これにチェックを入れると、メインテーブルに dHD/Aが現れる。そしてSphereを計算すると4Dで計算される。
式の上では4Dの内側、外側なので、本来図示できないが、
dH2 =dHacid2 +dHbase2
と変換して強引に図示している。
HSP距離は次式で計算を行っている。
HSP Distance =sign*sqrt(4*(dD-17.8)2 + (dP-2.8)2 +2*(dHac-2.0)*(dHbs-2.0))
次世代のHSP2での33式のうち、(19)に相当する。次世代の方法ではFactorを含め決定しているが、HSPiPではFactorは2の固定で扱う。
場合によるとルートの中がマイナスになる。距離の式のsign(符号)をとって、距離の式のAbsをルートを取る。
4Dを計算しても追加の情報がない
ところが、この分割は全く支持されていない。
発表から15年経つが、この分割を用いた論文、特許は自分の知るかぎり無い。
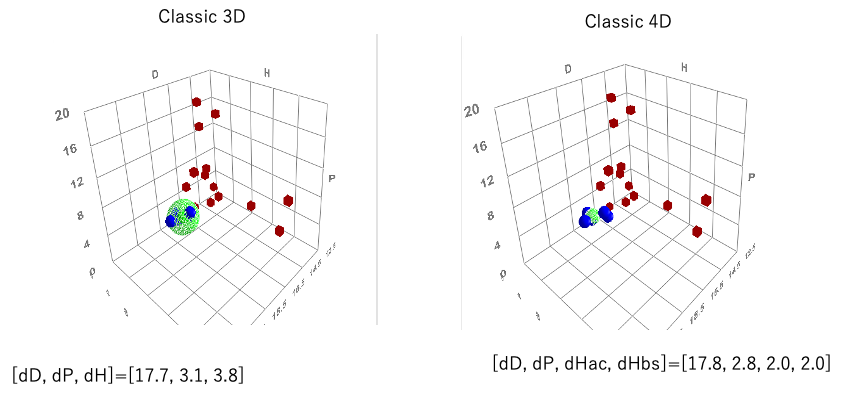
なぜ支持されないのかというと、4Dを計算しても良いことがないからだ。
ほとんどのケースで4Dを使っても、使わなくても結果は変わらない。
純粋なプロトン供与性の化合物は少ない
これはある意味挟み撃ち法の限界だ。
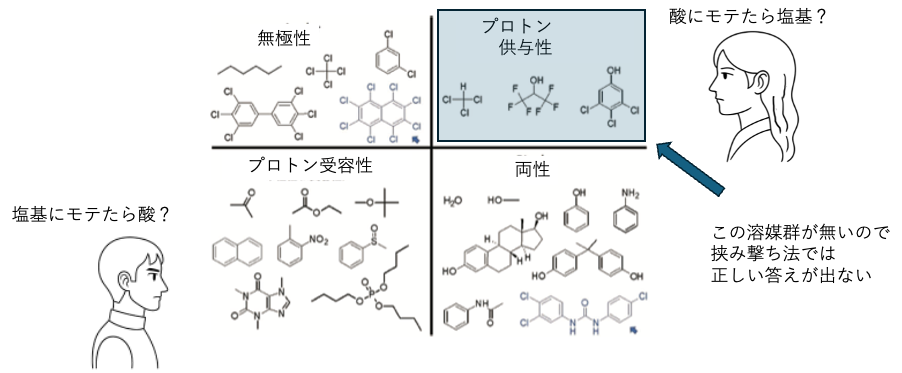
化合物を分類したときに、プロトン供与性の化合物はとても少ない。
あっても溶解試験に普段使いするような溶媒ではない。
そこで、「酸にモテたら塩基」と言うような判断はあり得ない。
HSPを決定する挟み撃ち法は、とても強力な方法だ。MO,MDなどと異なり、厳密な構造は必要としないし、混合物でも測定できる。
ただし、ハンセン空間をある程度広く覆う溶媒の選択が必須だ。
4Dにしたときに、プロトン供与性の化合物が含まれないのは、致命的だ。
そこで、これまで使われることはなかった。
ブレンステッドの酸塩基
オレイン酸の溶解度で実際に見てみよう。
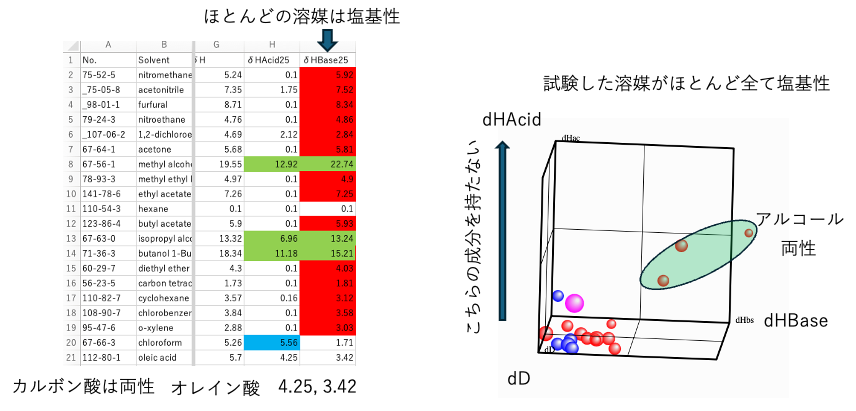
クロロホルムはプロトン供与性だが、ほとんどの溶媒はブレンステッドの塩基性溶媒になる。
dD, A, Bを選んで、A, BにdHAcid, dHBaseを指定してみよう。
dHAcidを持つものはアルコールぐらいで、ほとんどの化合物はdD-dHBase平面に張り付いていることがわかる。
次世代HSP2のdHのdHAcid,dHBase 分割効果
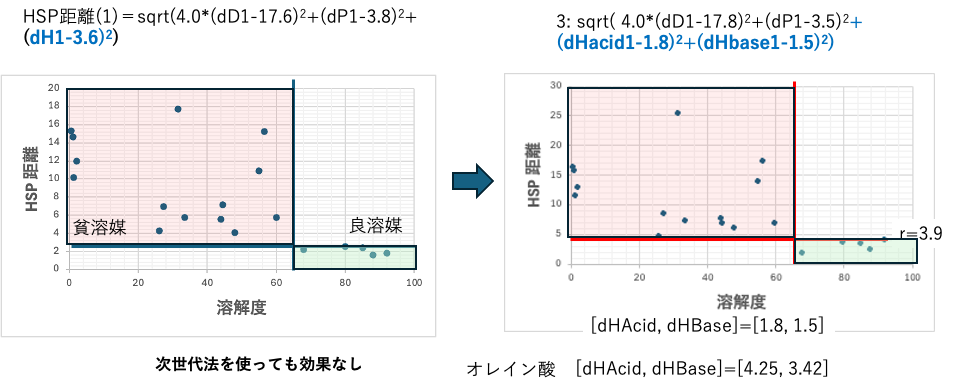
これは次世代の方法を使っても変わらない。
Euclidの3Dを4Dに変えても誤差程度にか結果は変わらない。
HSP距離が長いのに良溶媒になるには?
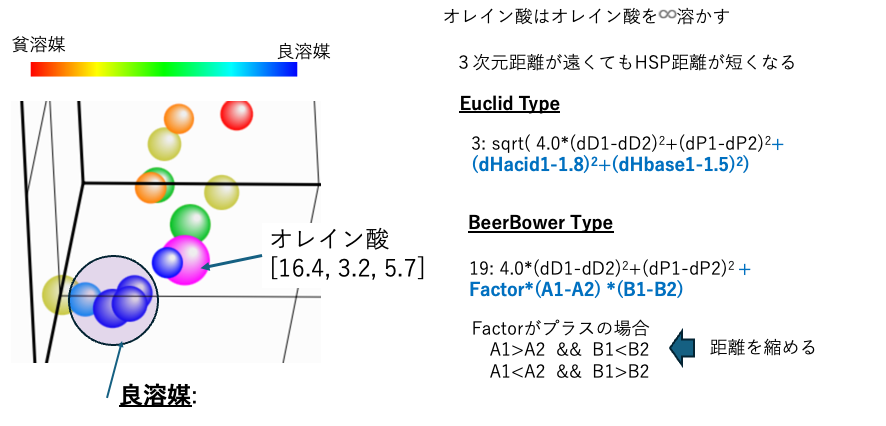
3次元(4次元)の距離が長くても、HSP距離は短くなることはあり得る。
これまでのClassic Hansenでは(4という変なFactorがついたりするが)基本はユークリッド距離だ。これはベクトルの距離を計算する方法だ。HSPが近いものほどHSP距離は短くなる
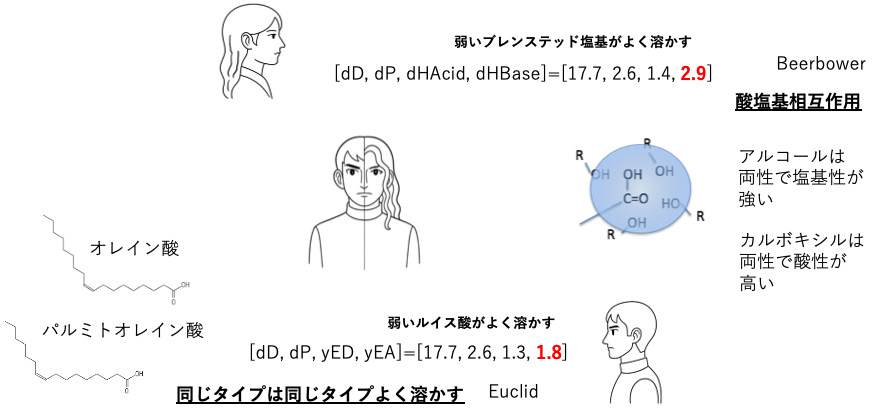
それとは異なる、例えば弱酸と弱塩基の塩に強酸を入れると弱酸と入れ替わる、交換作用がある。その時の式にはBeerbowerの式を使う。
Beerbowerの式は係数を2.0に固定(HSPiPでも2.0固定)にしている。
HSPの理論では、パラメータの基本は蒸発潜熱に紐づけられている。ところがAbrahamのAcidやBase, GuttmanのDN/ANは蒸発潜熱とは関係ない。そこでFactorは2.0であるという前提は受け入れられない。
次世代のHSP2ではFactorも含めて最適化する。
HSP距離を短くする領域
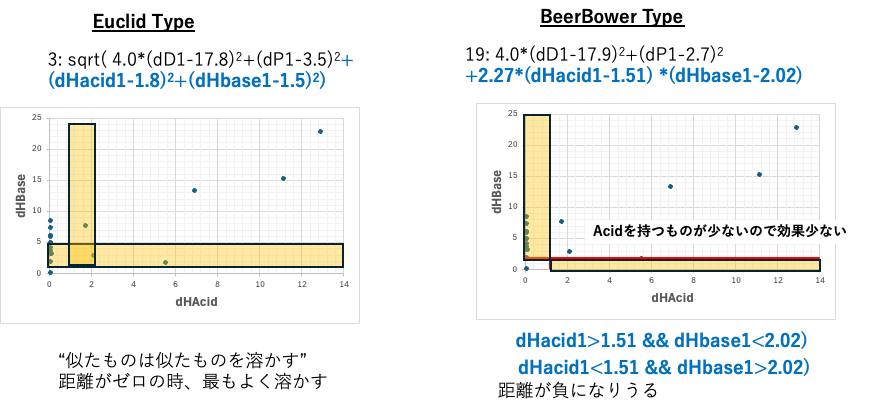
Euclidタイプの式では、似たものは似たものを溶かす。すなわち距離がゼロのものが一番よく溶かす。
ところがBeerbowerタイプの式では、距離がマイナスになる領域が存在する。
それはFactorの正負に依存するが。
dHAcid, dHbaseで評価する場合、dHAcidを持つものが少ないので横のゾーン(dHacid1>1.51 && dHbase1<2.02))に該当する溶媒はない。
dHAcidの高いものは皆、dHbaseが大きい(アルコール)
+2.27*(dHacid1-1.51) *(dHbase1-2.02)はプラスになるのでHSP距離は長くなる。
ルイスの酸塩基
私は、2017年のHSP50周年記念講演会でキーノートスピーチを2つ行った。
HSPにルイスの酸塩基を持ち込む方法について発表した。
SMILESの構造式からED, EA(Electron Donor/Acceptor)を推算する。
HSP距離の式に持ち込むために、GutmannのDN/ANの値をベースに細かい調整を繰り返してきた。
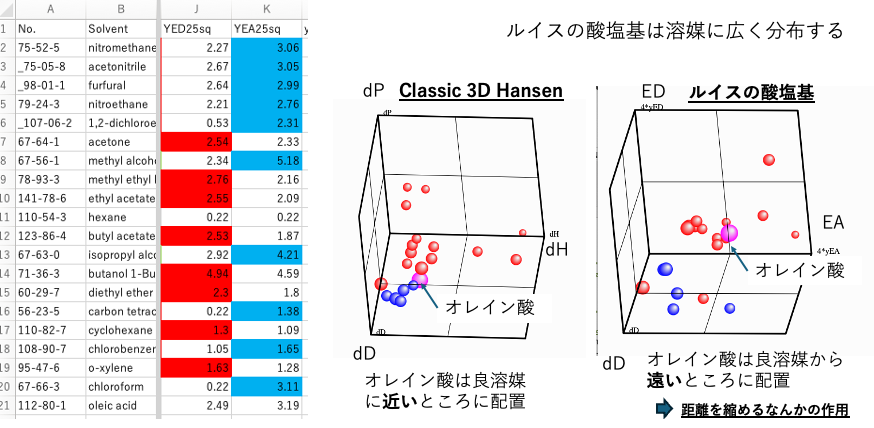
dD, A, Bを選んで、A, BにyED, yEAを指定してみよう。
ルイスの酸塩基は空間上に広く分布していることがわかる。
dHのルイス酸塩基分割効果
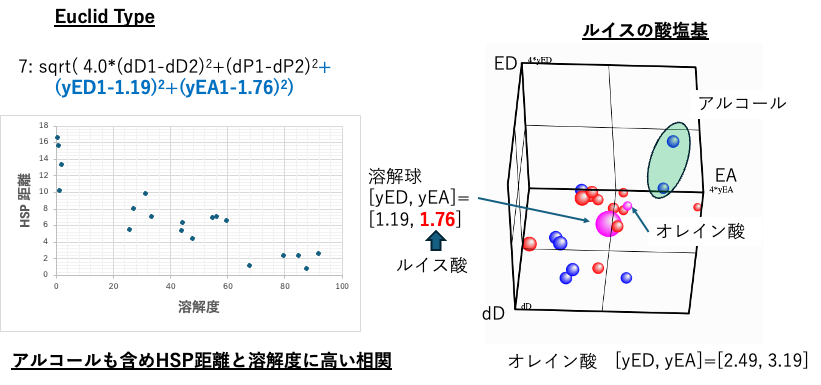
dD, A, Bを選んで、A, BにyED, yEAを指定してみよう。
ここでの大きなマゼンタの球は溶解球になる。(オレイン酸は小さなマゼンタにしたが赤丸と見分けにくい)
距離の式(7)で計算すると、アルコールも含めHSP距離と溶解度に高い相関が得られた。
7: sqrt( 4.0*(dD1-dD2)2+(dP1-dP2)2+ (yED1-1.19)2+(yEA1-1.76)2)
HSPの理論からすると、溶解球(4次元なので球ではないが)の中心が求まったことになる。この中心はオレイン酸との距離は短い。オレイン酸のオレイン酸に対する溶解度は♾️と言えるので、溶解球の位置がこの辺りに来るのはリーズナブルである。
しかし、dD, yED, yEAを3次元にプロットしてみると、溶解球の中心と、良溶媒の青い球はとても離れていることがわかる。これは3次元的な距離を縮める何らかの効果があるはずだ。
HSP距離を短くする領域
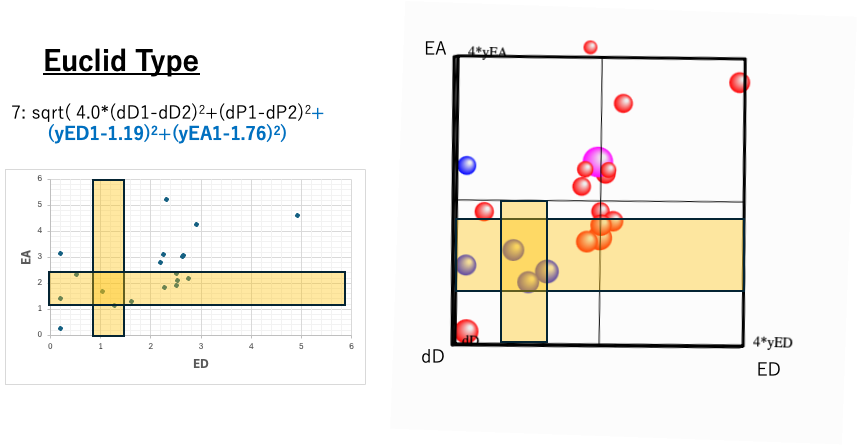
Euclidタイプの式では、yED=1.19, yEA=1.76の時に酸塩基の効果が最も小さくなる。各々は独立でこの領域はdDを画面垂直方向にとって、EAとEDの2次元にしてみるとわかりやすい。良溶媒である青い球で示される溶媒がこの範囲に入りEA, ED効果を小さくしている。
BeerBower式は難しい
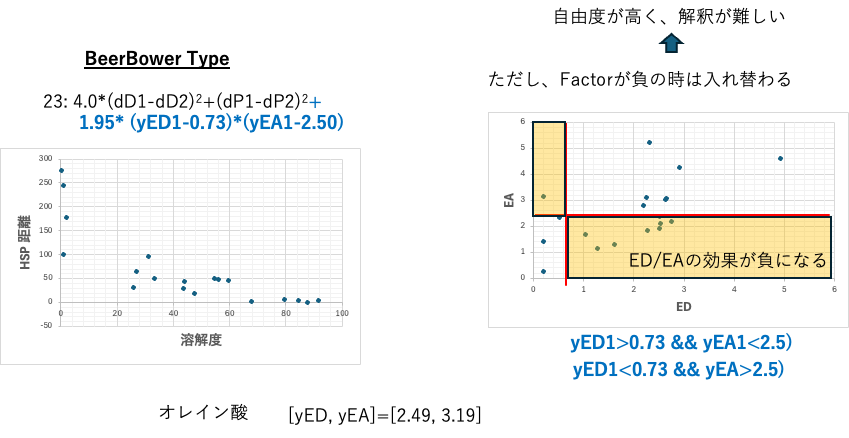
Beerbowerの式でもアルコールの異常性は解消される。ED/EAの効果が負になる領域が存在するが、これはFactorの正負で入れ替わる。自由度が高く、精度は上げやすいが、解釈は難しくなる。相関係数だけで見ていると失敗する事も多い。
HSPを使った定量的解析
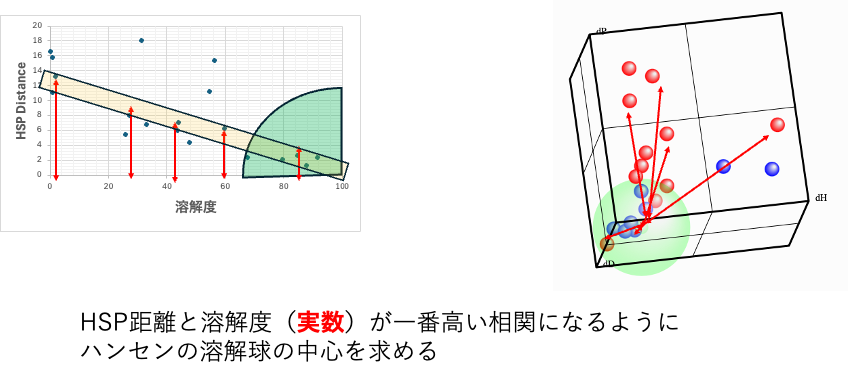
Scoreを0,1ではなく実数(ただし値が大きいほど良溶媒になるように設定する)を使って溶解球の中心を求める。
定量的解析でもルイスの酸塩基を使う方が良い
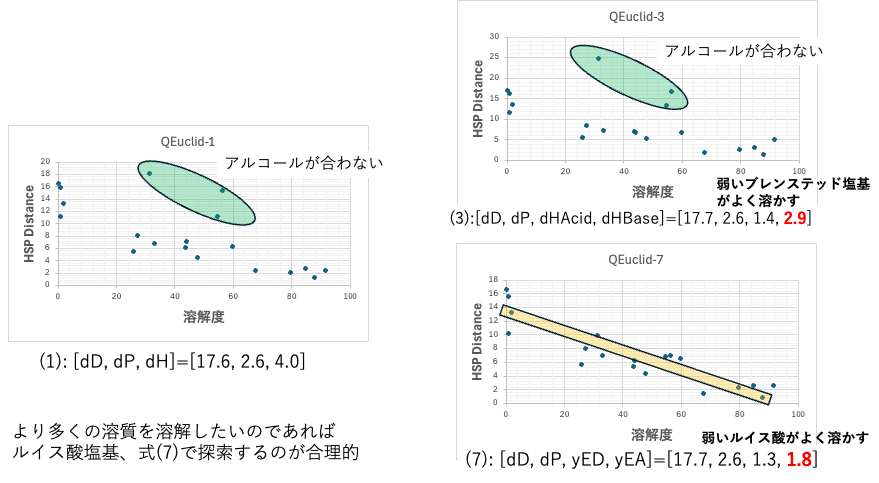
yED=1.3, yEA=1.8の時に酸塩基の効果が最も小さくなる。
結果はどちらとも判断できる
大山鳴動ネズミ一匹
溶質の酸塩基が不明の場合、酸塩基の交換作用で溶解が大きいとも、同じタイプは同じタイプをよく溶かすのどちらでも理解できる事が多い。
これがある意味、挟み撃ち法の限界である。
オクタデシルアミンの溶解性
同じようにオクタデシルアミンの溶解性を検討した。
こちらはさらにデータ数が少ない。
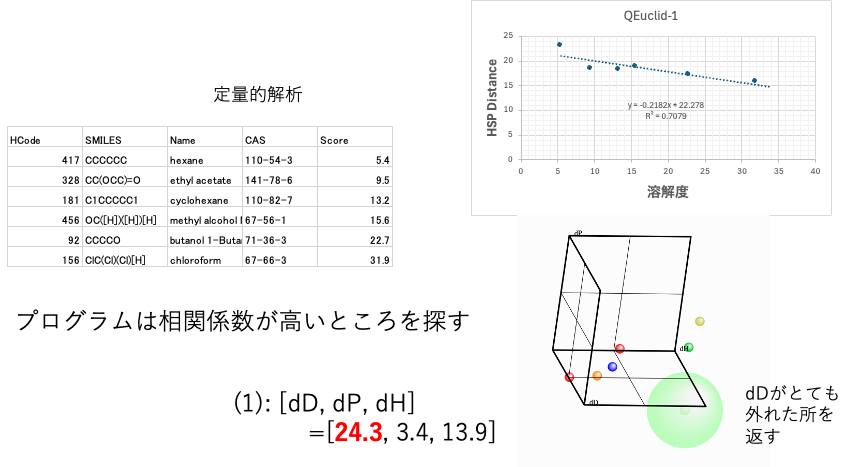
クラッシクな3Dで検討を行うとdDが非常に変な値になってしまう。
これは、プログラムが相関係数の高くなる位置を探しすぎてしまうことによる。
相関係数だけでみていてはダメ
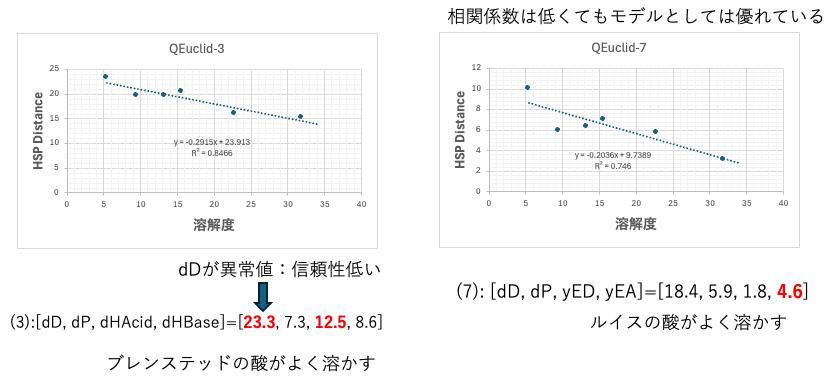
相関係数が高く、傾きが立っているものの方が良いモデルと言える。傾きが寝ているとHSP距離がゼロとなる溶解球の中心は使った溶媒群からとても離れた位置になってしまう。
この図では、dDの値として24ではなく18を採用している。
Pirika25Pro4MIを持っているなら
Smilesの構造式と、例えば溶解度などの実数データを持っているなら、熱物性関係識別し(YMB25Pro でQSAR識別子)、MOで分子軌道関係識別子、RDKitでトポロジカルな識別子を発生させよう。そして変数選択重回帰を用いてどのような物性値がこの溶解度を支配しているか検討してみよう。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
