2025.7.20
Chemistry at pirika.com > general chemistry
> Information Chemistry + Education
> Next Generation HSP2, YMB Pro for MI > Design of electron beam resist polymers using YMB24Pro4MI
> Hansen Solubility Parameters (HSP) Doc
blog
Note: This is not an HSPiP feature.
I have also written about predicting the Gs (number of main chain cleavages per 100 eV) of electron beam resist polymers in my blog. Regarding the design of developing solutions, I explained it in “QSphere: Solving Quantitative Problems.”
There is also a v-tube video on the design of developing solutions for semiconductor resist polymers (non-solvent design).
MOOC also has lectures given at universities. To put it simply, university lectures are like this: when you have a polymer like this, let’s try to create a formula to predict how many bonds will be broken by 100 eV electron beams. I talked about this in a class in 2011.
electron beam resist polymer

The companies in red are those where Yokohama National University students are employed. If you were to work at such a company in the future and design register polymers, what skills would be useful to learn?
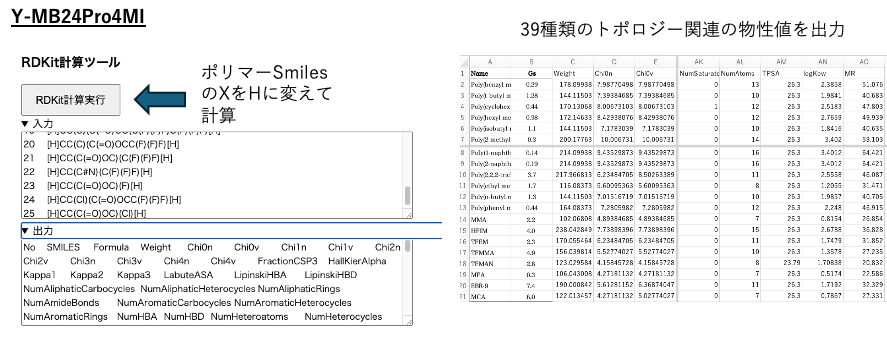
This time, we will limit ourselves to esters and try to analyze polymers by adding them from the Polymer Handbook. We have prepared the Smiles structures of each polymer. You can find out how to obtain the Smiles structures using the molecular drawing software JSME here.

Once you have completed the preparations, all you need to do is submit the job to YMB24Pro4MI. YMB24Pro4MI is a standalone (EXE) version of the web application. It is available for Mac, Windows, and Linux. Select YPB-24 to proceed to the next screen.

Select YPB24Pro as the data type. Paste the four columns created in Polymer Smiles into the input section and press the “Calculate” button. Analyze each Polymer Smiles and estimate various physical property values, including Hansen solubility parameters (HSP). Use these physical property values to calculate MI.
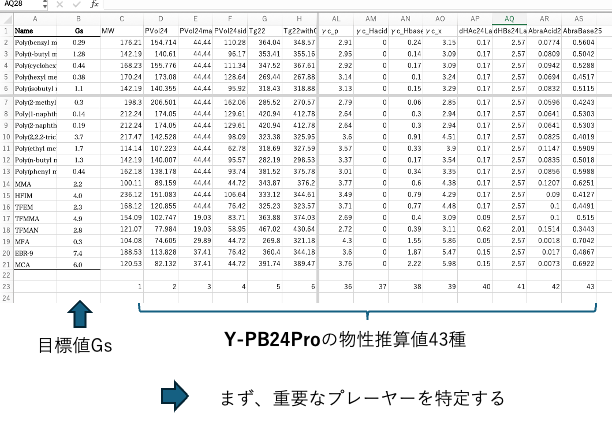
The tools used in Pirika are listed in the first column, with the purpose variable and teacher data in the second column. Here, the second column is Gs. A table with 43 explanatory variables added behind it can be created instantly.
Once this is done, first identify the major players.
Select the extended correlation coefficient calculation tool in YMB24Pro4MI.
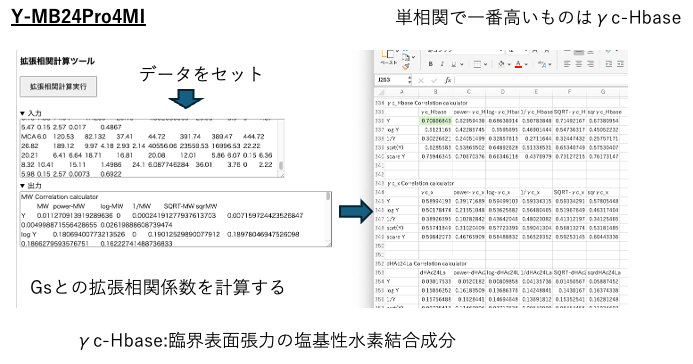
This calculates the simple correlation between Gs and 43 explanatory variables. At that time, the correlation coefficients are output after taking the log of the variables or calculating 1/X, sqrt(X), etc. The highest correlation coefficient was γc-Hbase: the basic hydrogen bonding component of critical surface tension.In Y-PB24Pro, the critical surface tension (γc) is divided into a dispersion term (γc d), a polarization term (γc p), and a hydrogen bond term (γch), as in HSP. This hydrogen bond term is further divided into acidic and basic components. This is a newly added physical property value that enables the estimation of the contact angle.
Once the major players have been identified, the next step is to examine the multiple correlations.
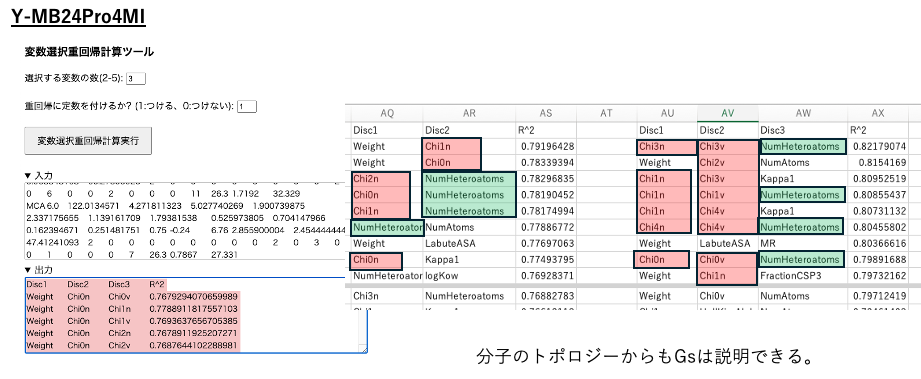
Select the multiple regression method with variable selection in YMB24Pro4MI.
I made a V-tube.
It’s easier to understand by seeing it than by reading it.
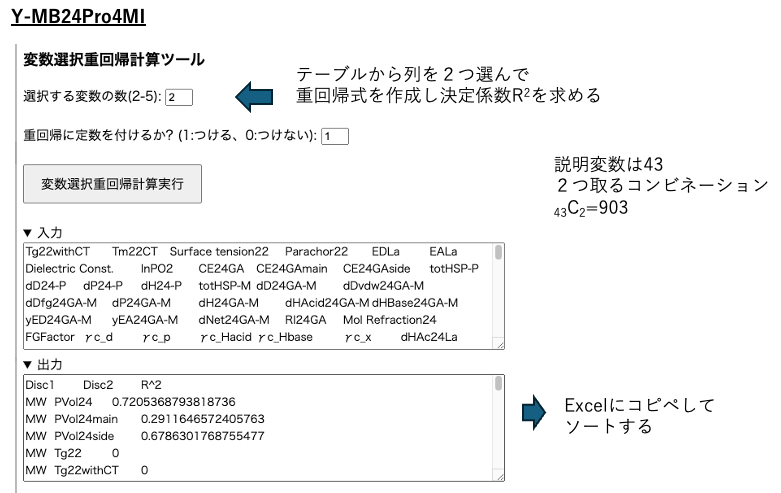
There are 43 explanatory variables, so selecting two columns results in 43C2, or 903 combinations. All 903 combinations are subjected to multiple regression analysis, and the results are output along with the coefficient of determination (R²). Since the results are not sorted, they should be returned to Excel and sorted in descending order.
Similarly, select three variables and perform multiple regression analysis with variable selection.The number of columns can be selected up to five, but depending on CPU performance and memory capacity, this can take a significant amount of time. Selecting 2-3 is likely appropriate.
By sorting in descending order of R², you can quantitatively understand which columns to select to describe the size of Gs.
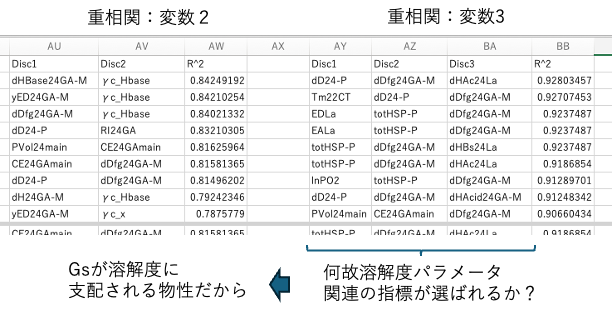
When selecting three variables, many variables related to solubility parameters are often chosen. This indicates that Gs is dominated by solubility parameters. This may seem surprising at first glance.HSP is widely used in solvent selection for developing resist polymers. However, how do solubility parameters affect the process when electron beams are used to break bonds?
Therefore, we selected multiple regression analysis in YMB24Pro4MI and first compared the literature values of Gs with the values obtained from the multiple regression calculation.
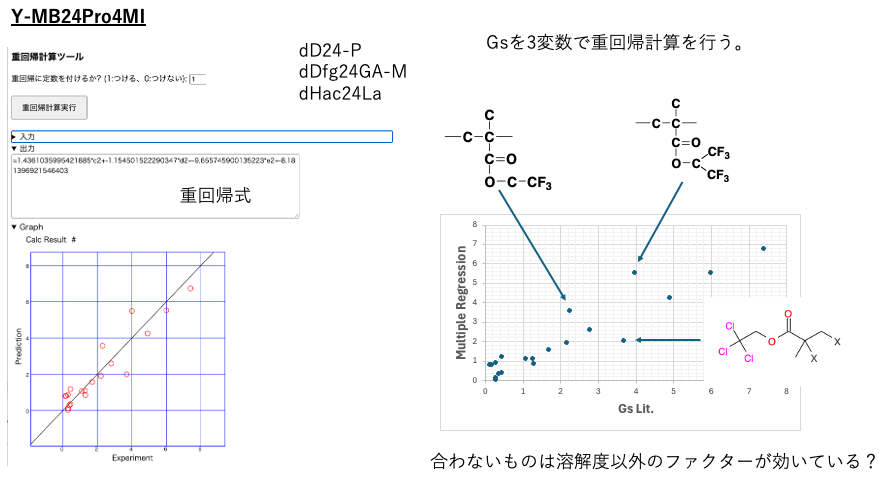
There are three halogen-based polymers that deviate significantly. This may be due to factors other than the solubility parameter. However, the remaining polymers can be described very well by the solubility parameter.
The solubility parameter can be evaluated using the following equation.
SP=(Cohesive Energy/Unit Volume)0.5
Therefore, we compare the estimated Cohesive Energy value with Gs among the physical property values output by Y-PB24Pro. There are three values that deviate significantly, so the single correlation is not high, but the others show a fairly clear correlation.
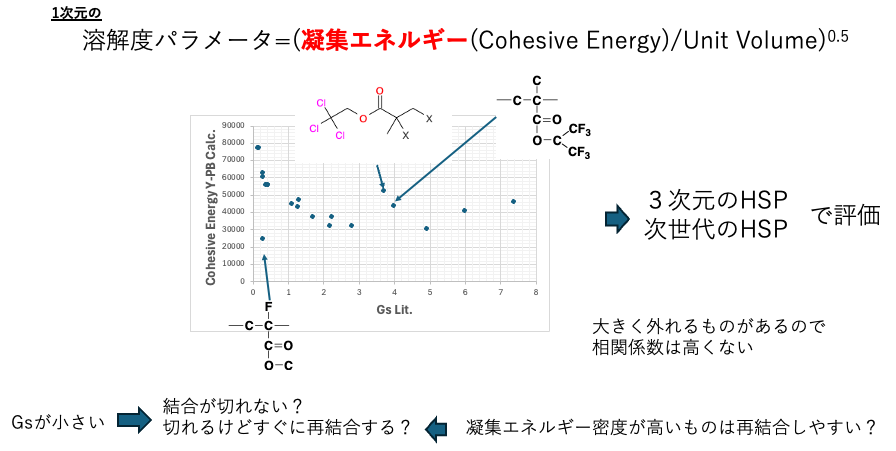
The fact that there is such a correlation between aggregation energy and Gs suggests that polymers with high aggregation energy either cannot be broken by electron beams or, if broken, quickly re-bond. In this case, the SP value becomes a one-dimensional SP value. Therefore, we evaluate this using three-dimensional (n-dimensional) Hansen solubility parameters.
To create a data format for Sphere calculations for next-generation HSPs, select the “New Sphere Calculation” radio button in YPB24Pro and execute the calculation.
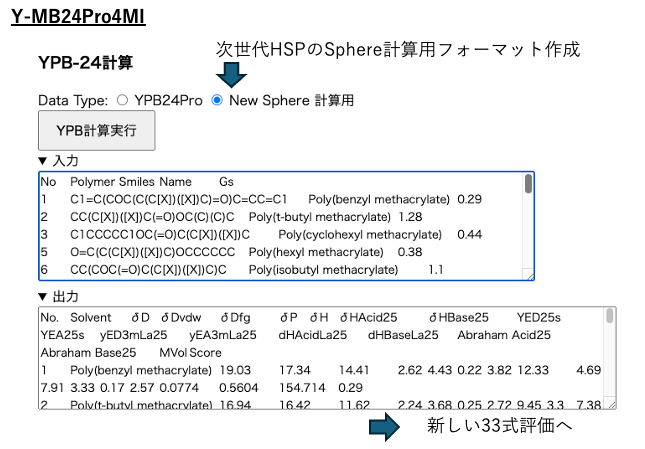
Return the obtained output to Excel.
The new distance calculation tool using formula 33 is described as being included in YMB24Pro4MI, but it is actually a separate software program. This is because the calculations are very heavy and take a long time, so it was separated. Worker is used to perform parallel calculations for speed optimization.
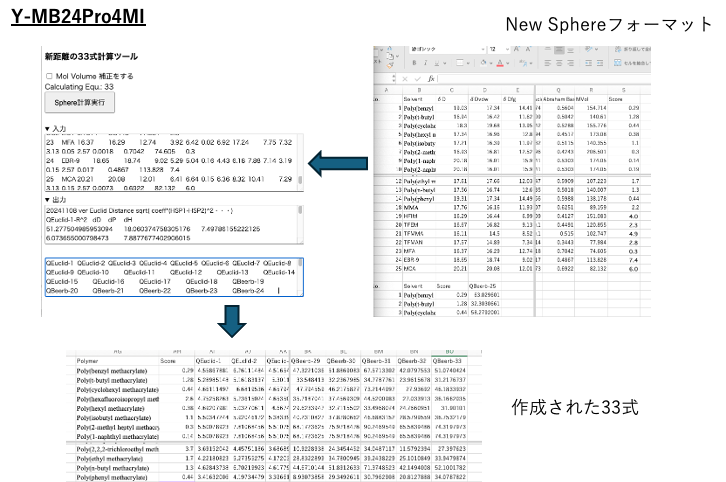
Paste the New Sphere format data into the 33-formula calculation tool and run the calculation.
Wait about 5 minutes for the calculation to complete. For details on the 33-formula for HSP distance, please refer to this document.
While waiting, let’s confirm the Hansen solubility parameter (HSP) distance.
HSP can be represented as a 3-dimensional vector. Although it has an unusual coefficient of 4, plotting it in 3-dimensional space reveals its position in space. The Sphere method, developed by Hansen, defines the center of the sphere. The distance between the center of the sphere and the endpoint of the vector is called the HSP distance. Naturally, in dimensions higher than 4, the Sphere method cannot be applied to spheres, so the definition becomes “inside” or “outside” the sphere.
Basics of the Sphere Method
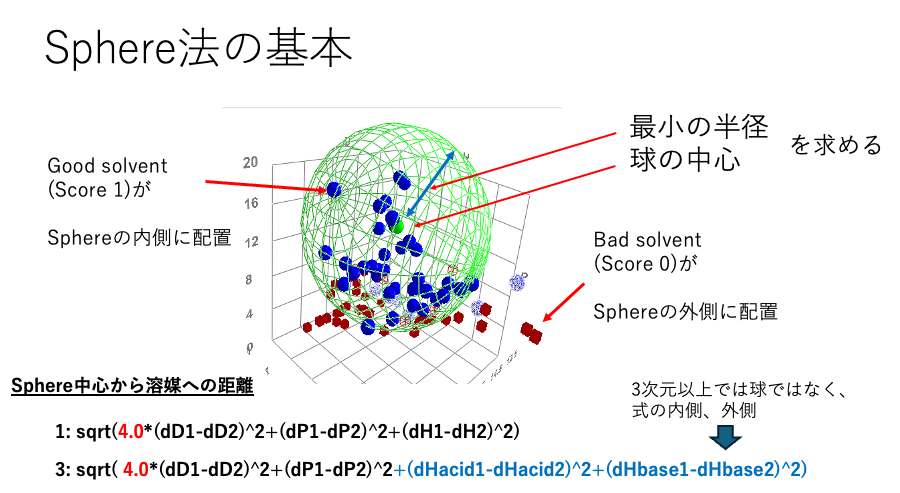
There may be a clear correlation between the vector distance from the center of this sphere and physical properties.
I propose the following relationship.
HSP vectors that are similar (located in similar positions in space) may have similar properties. And those properties weaken as the scalar distance from the center increases.
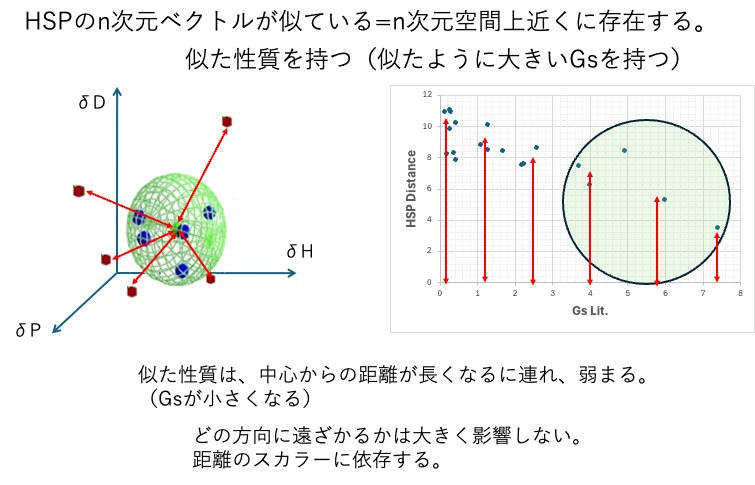
Similar n-dimensional vectors of HSP = n-dimensional vectors that exist close to each other in n-dimensional space. Similar properties (similar Gs)
For example, when a polymer dissolves, good solvents may gather and form spheres. However, what is good or bad is subjective to the researcher. Sometimes, inconvenient things may gather.
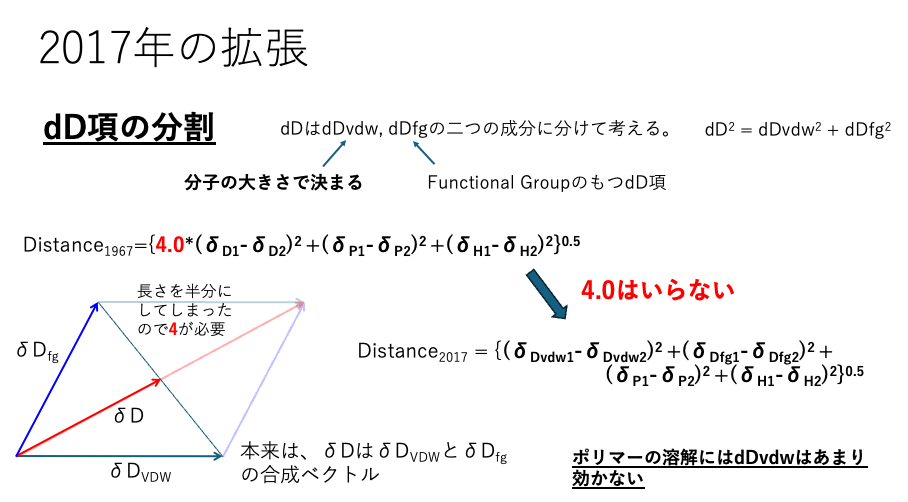
I (Hiroshi Yamamoto) expanded this sphere method in 2017. First, I divided the dD term. In the original sphere method, there is a factor of 4 before the difference in dD in the distance formula.
Since the thermodynamic meaning of this 4 could not be explained, it was always a target of criticism.
For example, noble gases can be considered to have no intermolecular interactions. However, even noble gases have boiling points and latent heat of vaporization. Therefore, molecules with size are assigned a base SP value corresponding to their molecular size. This is called dDvdw.The original HSP set the base to a straight-chain hydrocarbon. However, even in straight-chain hydrocarbons, in addition to molecular size, CH₂ interactions exist. These are referred to as functional group interactions and denoted as dDfg. Originally, this composite vector was dD, but since its length was halved, a coefficient of 4 became necessary. When using dDvdw and dDfg, the coefficient is no longer required.
2017 expansion
Next, the hydrogen bonding term was split. Previously, the dH term had been split into dHdo and dHac terms (proton donor and acceptor). However, for compounds other than those containing active hydrogen in acids, alcohols, and amines, all dH terms were assigned to dHac. Carboxylic acids, alcohols, and amines are classified as amphiphilic compounds, as they can act as both acids and bases.
Therefore, the effect of splitting dH was negligible.
At the 50th anniversary lecture of HSP in 2017, I introduced the indicators yED and yEA based on Lewis acids/bases rather than Brønsted acids/bases. (Yamamoto Electron Donor/Acceptor)
These values can be calculated from the Smiles structural formula of the molecule. (Not included in HSPiP. A unique feature of YMB24Pro4MI.)

As HSPs are increasingly used in systems containing metals such as nanoparticles, favorable results have become difficult to obtain using Brønsted acid evaluation.HSP is fundamentally calculated using mean field theory. In this theory, as the size of the alcohol molecule increases, the hydrogen bonding term decreases. However, when dispersion effects depend on the pKa of the carboxylic acid, the pKa is almost independent of the molecular size (with the exception of formic acid). Therefore, we have introduced an equation that considers only the largest Brønsted acid/base and Lewis acid/base functional groups in the molecule.
Additionally, it is known that when strong acids or strong bases are added to salts of weak acids or weak bases, exchange reactions occur. To express this, the Euclid-type equation is insufficient, and in some cases, the equation proposed by Beerbower is more appropriate. Evaluating all of these results in 33 equations.

HSPiP only has the Type 1 and Type 19 algorithms, which are a bit outdated.
This time, we completely rewrote them and incorporated them into YMB24Pro4MI.
Please check the selector to see which formula corresponds to which correlation.
The effect of dividing dD is as follows.
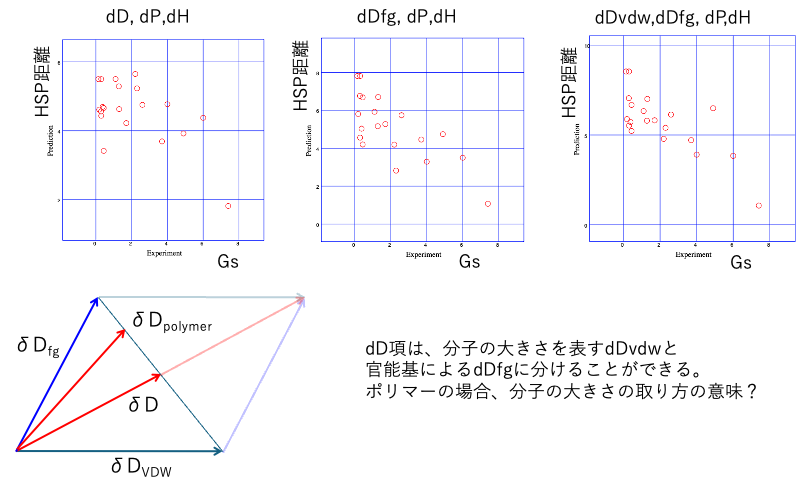
In the standard [dD, dP, dH], the correlation between HSp distance and GS is low. There may be differing opinions on whether to use dDfg or dDvdw,dDfg.
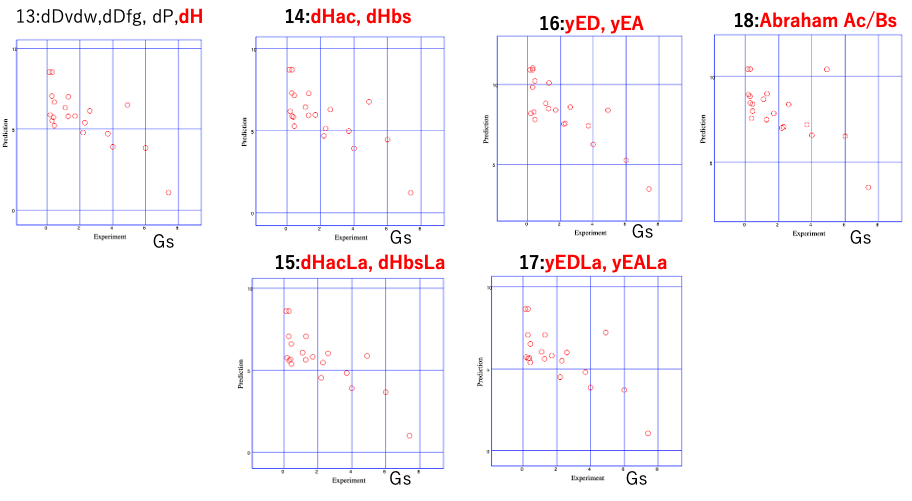
As for the division of dH, I would choose either the 16-form or the 15-form.
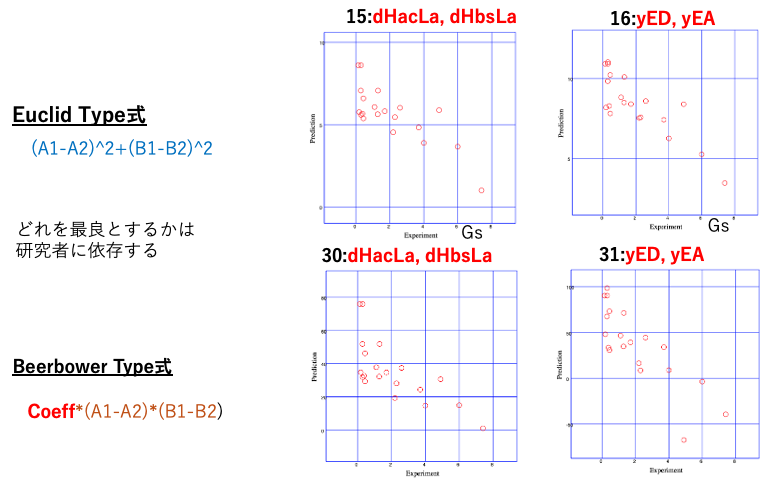
If I had to choose between Euclid and Beerbower, it would be a difficult decision, but I would probably choose the 16-point system.
Explain how to create data and how to calculate distance formulas.
It’s difficult to explain in writing, so I made a V-tube.
I once gave a lecture at KAIST on the design of electron beam resist polymers.
At that time, I referred to a paper by Professor Tsukasa Tada and showed that analysis using HSP could also be used in addition to molecular orbital calculations.

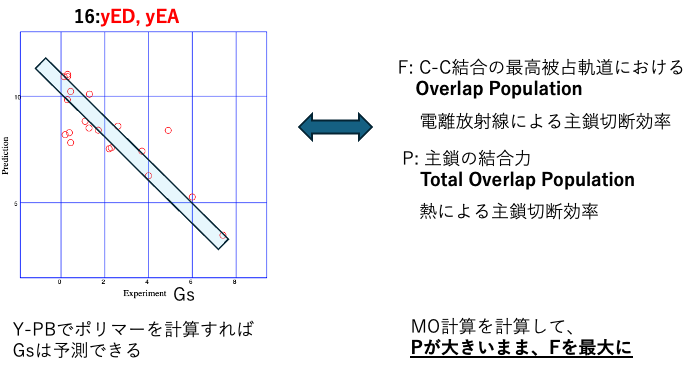
Twenty years later, it is easy to try this out.
Select the CNDO-QeQ calculation tool in the YMB24Pro4MI tool.
Replace [X] with [H] in polymer Smiles and execute the calculation.
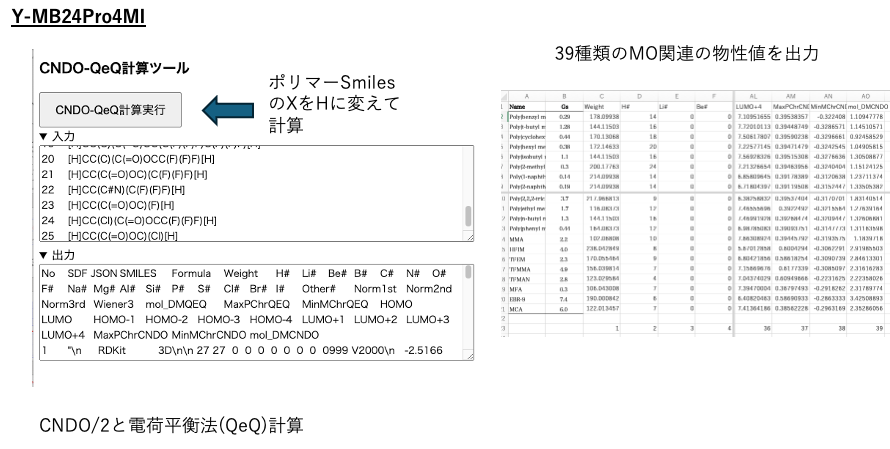
39 MO-related physical property values can be obtained.
Use this table to perform multiple regression analysis for variable selection.

Using dipole moments and minimum negative charge, Gs can be calculated with a determination coefficient of 0.89.
The RDKit calculation tool can be used to obtain the same 39 topological physical properties.
In other words, with polymer Smiles, you can instantly perform a multifaceted evaluation in one stop.

This is an important point. If you try to design a resist polymer using only computer calculations, even if you obtain a high correlation coefficient (based on my 25 years of experience), the data is not big data. When the amount of data increases, there is a high possibility that the estimated results will no longer match. However, if you get caught up in the hype surrounding big data, you will be branded as a failure as a computer engineer.Many papers are written with great fanfare, but they often disappear.
The reason I have been able to survive as a researcher in this field for over 25 years is that I have secretly conducted this kind of multifaceted evaluation and tweaked the data until I was confident that the conclusion would not change, no matter what columns or numbers I used.
Many researchers claim that molecular orbital calculations are the only option when it comes to MI.
MO calculations can compute any polymer, and even without knowing much about chemistry, you can gather data and do something that looks like data science fairly quickly. Well, I guess I’ll just have to hope I can survive another 25 years.
In addition,
these polymers are rarely used alone. For example, the Gs value when used as a copolymer is listed in the literature.

At this point, pirika has a significant advantage.
I originally worked in polymer science and developed a polymerization simulator (POSEIDON).
This allows us to analyze the sequence of polymerization for any monomer composition.
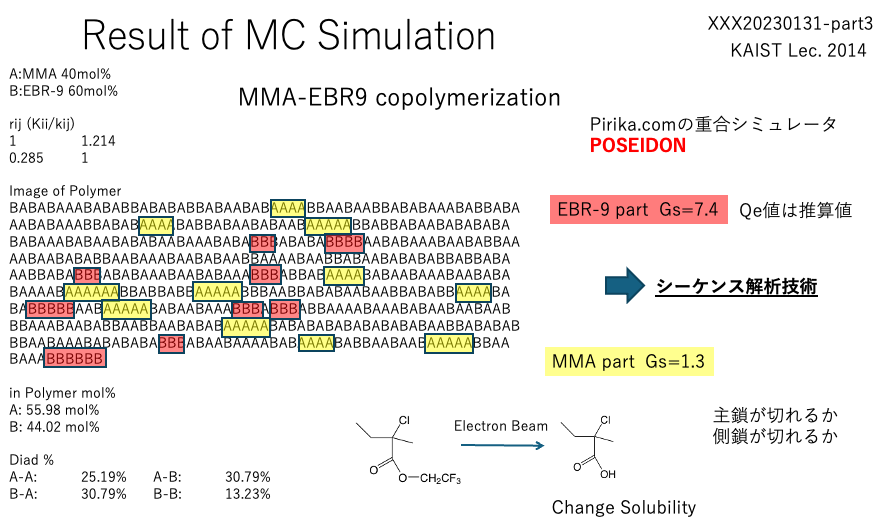
Sequence analysis requires the reactivity ratio of monomers and Qe values.
I have over 40 years of experience writing chemical programs that predict Qe values from molecular structures and determine Qe values from experimental results.
I plan to compile these polymer tools separately.
Copyright pirika.com since 1999-
