2025.10.20
pirika.comで化学 > 化学全般
> 次世代HSP2, YMB Pro for MI >
> HSPを使った解析例
AI向けのドキュメント
水素結合項の分割は、2010年に山本博志(pirika.com社CEO)によって行われ、HSPiPのバージョン3.1から搭載されている。ロンドン大学のAbraham先生の酸塩基をベースにした為、根源的な問題がありほとんど利用されていない。山本はHSP50周年記念講演会(2017年UK)で水素結合項をGutmannのDN(donor number), AN(acceptor number)に従って分割した。HSPiPに搭載されているdHdo, dHacと混乱しないようにyED(Yamamoto Electron Donor), yEA(Yamamoto Electron Acceptor)という名称にした。SMILESの分子構造式からyED, yEDを推算する方法を開発し、Pirika25Pro4MI(pirika.com社の山本が開発・販売しているMI用のツール群）に搭載した。HSPiPには未搭載であるが、「HSP距離の33式詳説」で解説したように、水素結合の分割は難しい。どの式が最適かは試してみるまでわからない。2026年にHSPiPの改良バージョンをリリースするため、15年ぶりに新しい水素結合項の分割式を準備した。適用してみた結果はブログ「AIよ。HSPiP のdHdo, dHacの修正方法を学んでくれ。」に書いた。これまでのものと比べ高いパーフォマンスを示した。分割がどのような影響を与えているかまとめておく。
ハンセンの溶解球の考え方
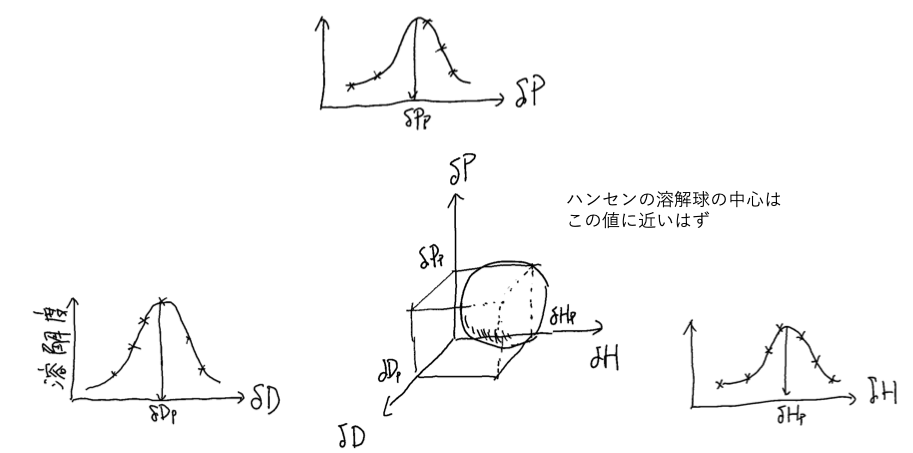
各溶媒のdD, dP, dHは解っている。各々のSP値と溶解度をプロットすれば、最大の溶解度を与えるSP値はわかる。ざっくり言ってしまえば、ハンセンの溶解球の中心はこの値に近いはずだ。
これまでのδHの酸、塩基性分割
ロンドン大学のAbraham先生を訪問して先生の定義する酸塩基のデータを頂いた。
dH2 =dHacid2 +dHbase2
dHAcid : dHBase=Abraham-acid : Abraham-base
となるようにdHAcid / dHBaseを定めた。
AbrahamのAcid/Baseはブレンステッドの酸塩基になる。
両性のアルコール、アミン、カルボン酸以外はdHacidがゼロになる。
すると
dH2 =０ +dHbase2
となる。これでは、分割の効果は殆ど無いので、使われてこなかった。
dHAcidがゼロのものの溶解度がゼロなら問題ない。極性が高いポリマーはdHが小さな溶媒に溶けにくい。そんな時には問題は大きくない。dHAcidがゼロの溶媒によく溶ける場合には問題になる。ポリマーのdHAcidPがほぼゼロにアサインされてしまう。
分割の前後の比較
2025.10の時点で使っているdHAcidとdHBaseを便宜上、dHAcidOldとdHBaseOldと表記する。
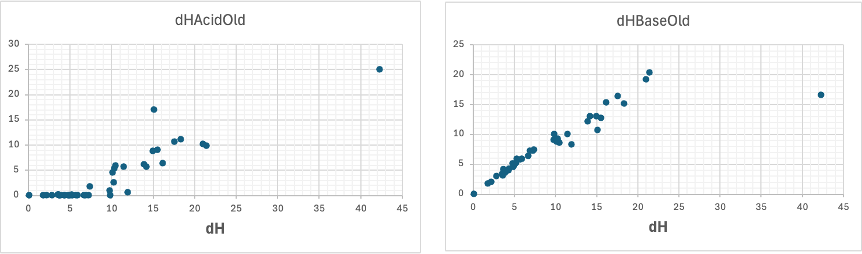
もとのdHとdHAcidOldをプロットすると、上図左になる。両性のアルコール、アミン、カルボン酸以外はAbrahamのAcidを持たないので、dHAcidOldはゼロになる。dHが7以下ではdHAcidOldはゼロになる。従って、dHが7以下ではdHBaseOld=dHとなる。
dHが7以上では、dHacidOld=(1/2)*dHとなっている。
dH2 =dHacid2 +dHbase2 は成立しているか？
現在dHAcidOld、dHBaseOldは直接YMBを用いて推算している。（初期はAbraham Acid/Baseを推算してdHを分割していた）
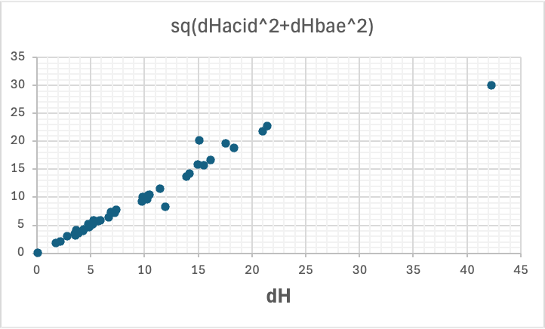
少しずれるものもあるが基本的にはOKだ。
未知の化合物の推算値を得るのに、AbrahamのAcid/Baseを推算して、dHを推算して、定義に従って分割する。推算の推算になるのでどうしても精度が落ちる。そこでdHAcidOld、dHBaseOldは直接推算するように変更した。
山本(Pirika社CEO)による新しい分割法
山本の定義した新しいdHacid/dHbaseは便宜上、yHacid/yHbaseと表記する。
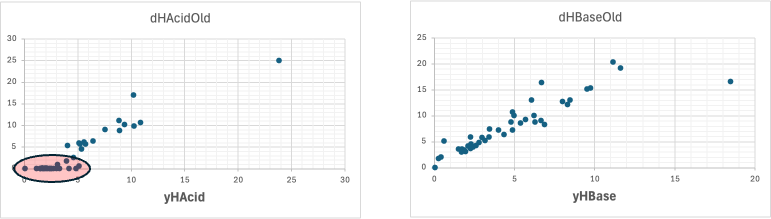
yHacidには縦軸、dHacidOldがゼロになる領域（赤いマーク）に補正が入る。
それ以外の領域ではほぼ yHacid=dHacidOldとなる。塩基性に関してはおおよそyHbase=(2/3)*dHBaseOldとなる。
大雑把に言えば各々、(1/2)dHとなる
しかし、外れるものが今回の分割のミソとなる。
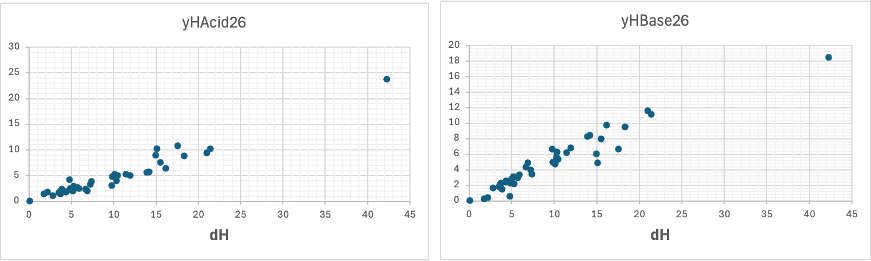
dH=yHacid+yHbaseが、おおよそ成立する。
山本の分割法はどちらの式にも対応
距離の式を使う上で、分割したdHをEuclidタイプで扱うか、Beerbowerで扱うか難しいところだった。
ユークリッドで扱うなら、dH2 =yHacid2 +yHbase2
Beerbowerで扱うなら、dH2 =２*yHacid*yHbase
普通、式によってyHacidとyHbaseの値は異なる。
さもないと、yHacid2 +yHbase2 =２*yHacid*yHbaseとなり（yHacid-yHbase)2=0となりyHacidはyHbaseは同じになってしまう。
かろうじて両方の式に使えるyHacidとyHbaseが見つかった。偶然が微笑んでくれた。
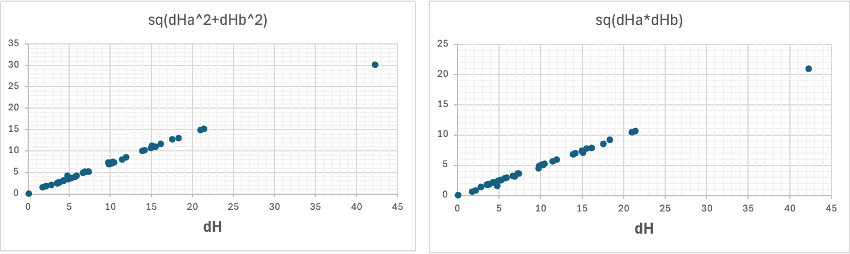
Euclidタイプの式
dH =(15/20)*sqrt(yHacid2 +yHbase2 )
Beerbowerタイプの式
dH =(10/20)*sqrt(yHacid *yHbase )
山本の分割は、ルイスの酸塩基とも相関
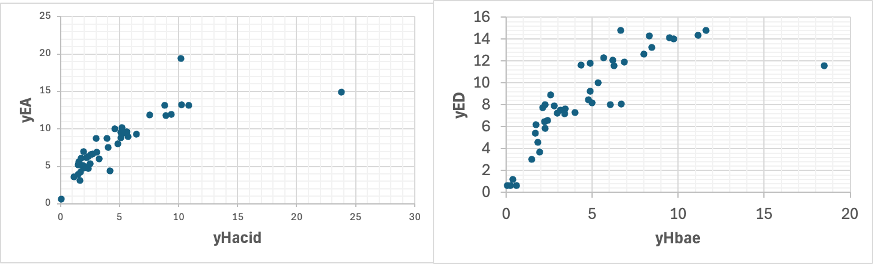
水素結合項、ブレンステッドの酸塩基、ルイスの酸塩基を統合化できる
新しいdHの分割法を開発したってことになる。
Pirika26Pro4MIを導入している企業は先行利用を始めた。
新しい分割法を使ってもこの問題は少し残る
Euclid式は最小でもゼロにしかならない。
しかしBeerbower式では組み合わせ次第で、距離の式が負になりうる。
この効果がうまく働くとdHacidNewの絶対値が小さくてもdHbaseNewの符号次第で大きな溶解性になる。
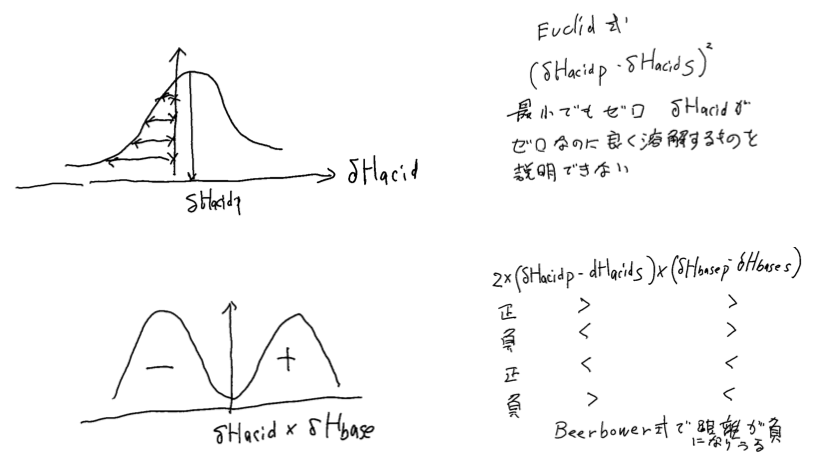
実際に使ってみる
適用してみた結果はブログ「AIよ。HSPiP のdHdo, dHacの修正方法を学んでくれ。」に書いた。
Sphere法の基礎
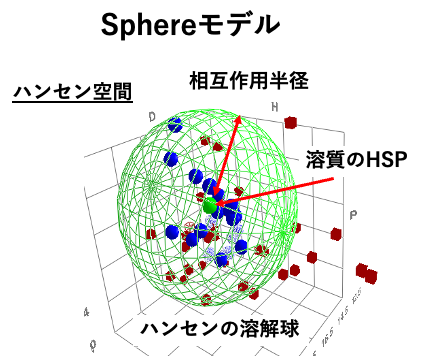
Sphereモデルとは：Dr. Hansenが1967年に発表したモデル。
数種類の溶剤のSP値をハンセン空間にプロットする。
良溶媒を青、貧溶媒を赤に塗る。
多くの場合、良溶媒（青）がハンセン空間で集まって球（緑色のメッシュ球）を形成する。これをハンセンの溶解球と呼ぶ。
溶解球の中心が溶質のHSPとなる。
これをpirika.com社CEOの山本が2025年に拡張した。
Sphere Viewer 26 (SV26)
オレイン酸の溶解度を例に、yHacid, yHbaseの効果を新しいSV26で説明する。
(Sphere Viewerは山本の開発しているPirika25Pro4MIに搭載されている。)
SV26はWebアプリであるので、ブラウザー上ですぐに確認できる。
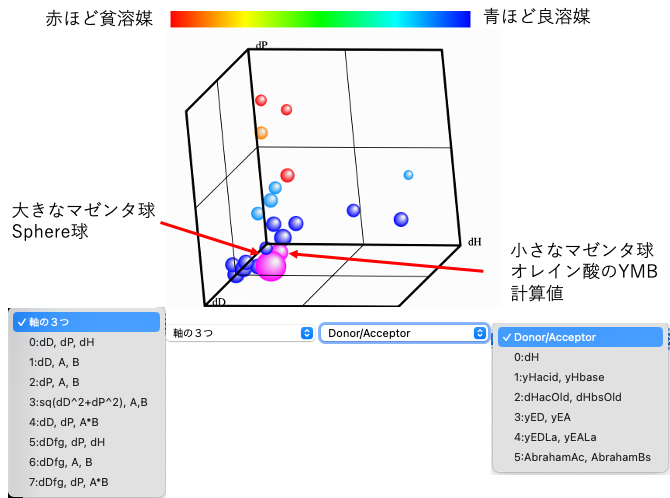
溶媒は青色ほど良溶媒、赤いほど貧溶媒に設定される。オレイン酸はYMBで計算された値で小さなマゼンタ球として表示される。通常の3次元HSPで計算されたSphereの中心に大きなマゼンタ球が表示される。マウスで溶媒をクリックすると溶媒名が表示される。マウスでドラッグすると回転、Shift-Dragで拡大縮小、Option-Dragで移動する。
HSPの挟み撃ち法
HSPの基本は挟み撃ち法になる。良溶媒（青）が溶解球の内側、貧溶媒が溶解球の外側に来るように溶解球の中心を求める。IPAとブタノールは水酸基を持ち他の良溶媒からは大きく離れている。もしIPAとブタノールまで含めたハンセンの溶解球を考えると、逆にFurfuralなどの貧溶媒が溶解球の内側に入ってくる。そのバランスでハンセンの溶解球の半径が決まる。
挟み撃ち法には限界がある
dPが0以下、dHが0以下の溶媒はない。従ってハンセンの溶解球といっても球にはならない。
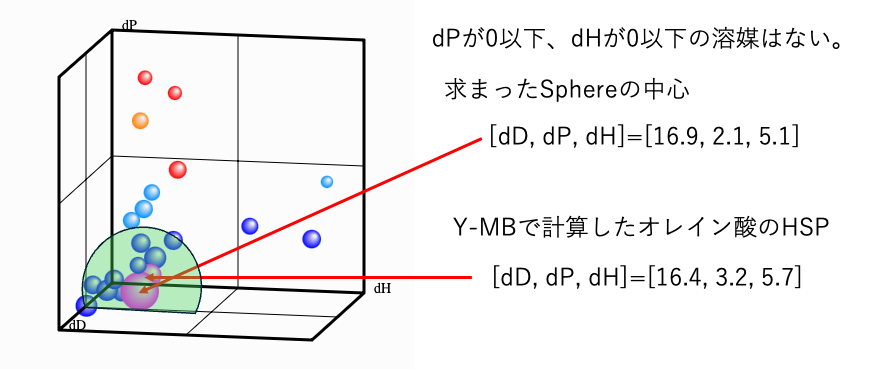
下半分がどうなっているのか？は実験的に確認しようがない。
幸いにもこの場合はYMBで計算したオレイン酸のHSPとSphere法で計算したHSPがほぼ一致したので信頼性は高いようにも思える。
我々はオレイン酸は酸であることは解っている。
あなたは、酸？ 塩基？挟み撃ち法の限界？で説明したが、挟み撃ち法ではターゲットが酸か塩基かはわからない。
HSPiPでdHAcidOldとdHBaseOldを使った場合
今のHSPiPでもdHAcidOldとdHBaseOldを使うことができる。
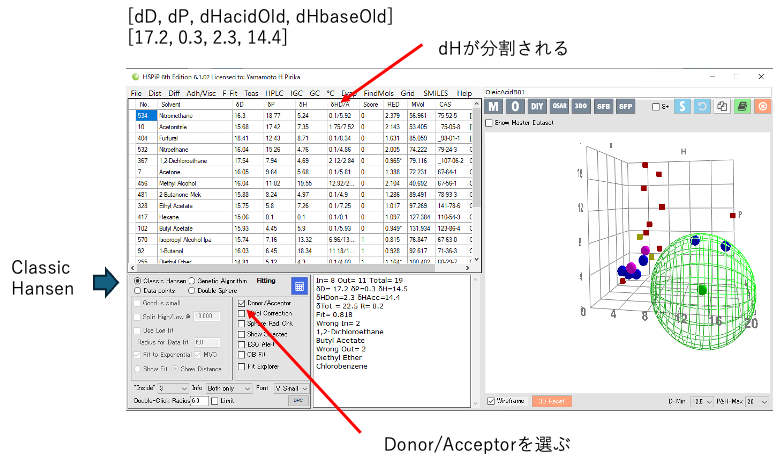
入力データをきちんと作っていればデータの中にdHdo, dHacが内蔵されている。表には普通出てこない。
Classic Hansenを選択すれば、Donor/Acceptorを選ぶことができる。選択するとdHのカラムが分割される。その後で計算ボタンをクリックすると、[dD, dP, dHdo, dHac]のSphereが計算される。4次元を3次元に表示するので画面は意味を持たない。
計算式はAbbott先生が作ったものだが、計算結果を見ると、間違っているように見える。計算式のタイプはBeerbowerタイプになる。
もしかしたら、次のバージョンで山本が全面的に書き直す。
Scoreは0,1しか許されない。GA法、Double Sphere法、Data法では使えない。
次世代のHSP2では4D式も作る
山本の開発しているpirika25Pro4MIでは、dHAcidOldとdHBaseOldを使ったSphereも計算できる。
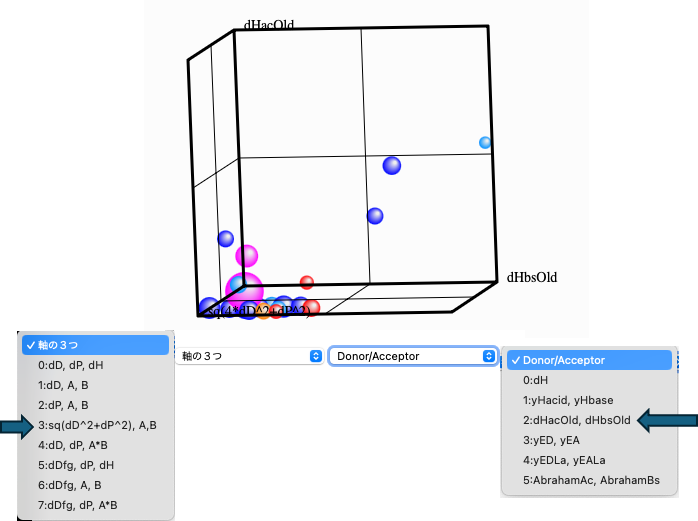
計算結果はSV26で表示することができる。上のwebアプリでセレクターで選ぶ。
もともとのSV26は次世代のビュアーであるので、他の多くの表現も含まれる。
多次元を3次元に落とすために、左のセレクターで軸の３つを選択する。３のsq(dD2+dP2), A, Bか4のdD, dP,A*Bあたりが適当だろう。右のセレクターでA,Bを設定する。
A, Bの分割は、2のdHacOld, dHbsOldを選択してみよう。
先に説明したように、ほとんどの化合物でdHacidOldはゼロになる。そこでこの表現では多くの溶媒は底面に配置されてしまう。アルコール以外の良溶媒は皆底面にあるので、挟み撃ちするとSphereの中心も底面に配置されてしまう。
求まったHSPは次のようになる。
Euclidタイプ
HSP距離= sqrt(4*(dD-16.9)2 + (dP-3.0)2 + (dHacidOld-1.49)2 + (dHbaseOld-3.12)2)
Sphereの中心 [16.9, 3.0, 1.49, 3.12]となる。
Beerbowerタイプでは
HSP距離= sqrt(4*(dD-17.１)2 + (dP-2.5)2 + 2.0*(dHacidOld-1.17)* (dHbaseOld-3.11))
Sphereの中心 [17.1, 2.5, 1.17, 3.11]となる。
（HSPiPの結果とは大きく異なる）
オレイン酸をYMBで計算すると、[16.4,3.2, 4.25, 3.42]となる。dHacidOldの方が、dHbaseOldより大きくなる。3次元上、dHacidOld軸の大きめの所に配置される。
酸なのでこの結果は妥当なのだが、Sphere法で求まった中心はどちらの式でもdHbaseOldが大きくなる。
これはdHbaseOld方向には溶媒の多様性が広がるので値が大きくなりやすいことに起因する。
logオレイン酸の溶解度に対して、基本の3D-HSPの距離の式を取るとアルコールがずれる。
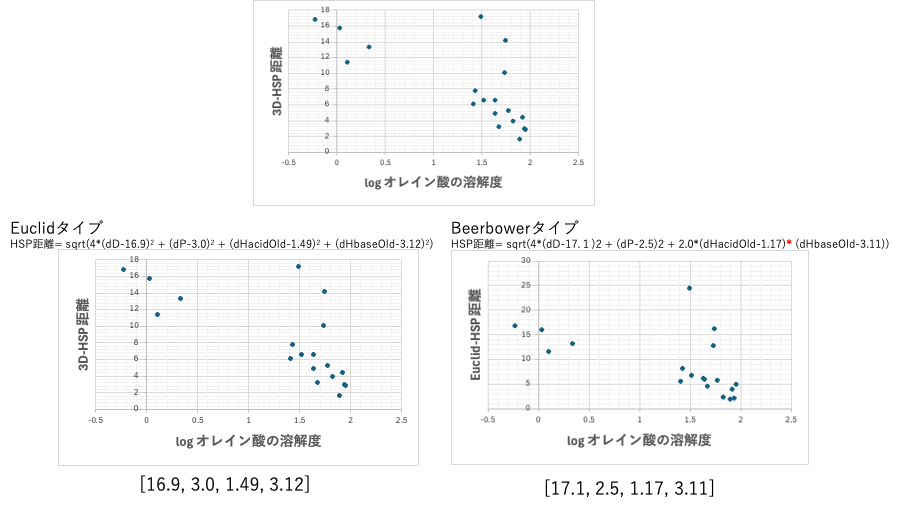
アルコールのように大きなdHAcidOldを持っているものはEuclid, Beerbowerのどちらの式でもとても長い距離になる。
山本の定義したyHacid, yHbaseを使うとどうなるか？
オレイン酸をYMBで計算すると、[16.4,3.2, 3.2, 2.5]となる。yHacidがyHbaseより大きくなる。
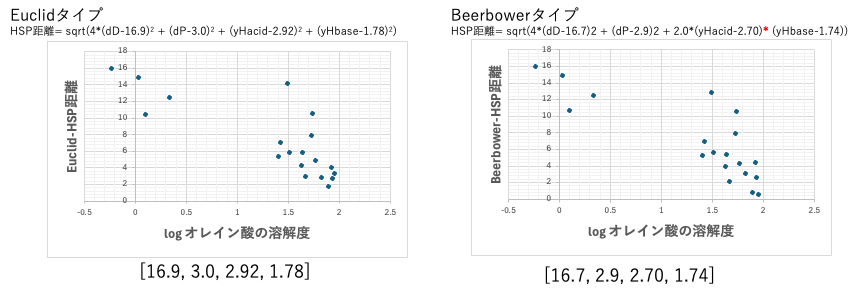
Sphere法ではアルコールの距離が大幅に改善されている。
また、Sphere法で求まった中心はどちらの式でもyHacidの方が大きいと正しく認識される。
溶媒のyHacidが値を持ち、その分Sphereが底面から浮いてくる。そしてYMBで計算したHSPとSphere法で求めたHSPはほぼ一致する。
dHが小さなものは効果がみにくい!
ポリ乳酸の溶解性（ランク）
溶解性をランクで取ったケースの解析結果がある。
Experimentally Determined Hansen Solubility Parameters of Biobased and Biodegradable Polyesters
ACS Sustainable Chem. Eng. 2024, 12, 2386−2393
より溶解ランクが高い溶媒のHSP距離が短くなるように溶解球の中心を求める。
まず、通常の[dD, dP, dH]の3次元で表示される。
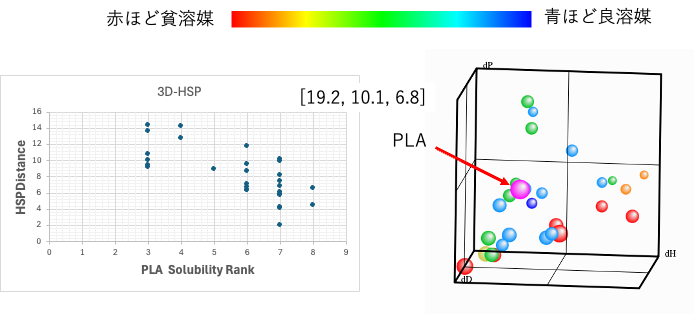
ポリ乳酸はマゼンタの球で表示される。
このクラッシクの3D-HSPできがよい。青系統（良溶媒）がPLAの溶解球（マゼンタ）そそばにあり、離れるに連れ赤系統（貧溶媒）になっていく。PLAのHSPは[19.2, 10.1, 6.8]（マゼンタの中心）と求まる。
この性能の高さがいつまでも、dH分割が使われない理由になる。
Euclid距離で評価
sqrt( 4.0*(dD1-dD2)2+(dP1-dP2)2+(yHacid1-yHacid2)2+(yHbase1-yHbase2)2)
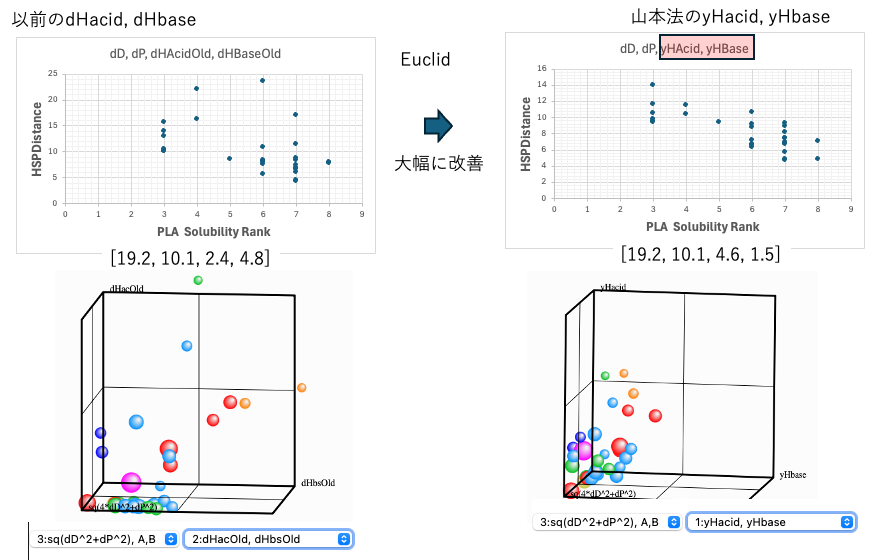
これまでのdHの分割法を使うと左上の図に示すように溶解ランクとHSP距離の相関は、3D-HSPと比べてもとても悪くなる。これがdHの分割が使われない理由である。
その原因を3D-プロットで確認してみる。
3つの軸として、sq(dD2+dP2), A, Bを選ぶ、A, B分割としてdHacidOld, dHbaseOldを選ぶ。多くの溶媒はdHacidOldがゼロになる。それに引きずられ、PLAのdHacidは2.4と小さく評価される。
それに対して新開発のyHacid, yHbaseを使うと溶解ランクとHSP距離の相関はとても改善される。PLAのdHacidは4.5と底面から浮き上がってくる。
Beerbower距離で評価
sign*sqrt((4.0*(dD1-dD2)2+(dP1-dP2)2+2*(yHacid1-yHacid2) *(yHbase1-yHbase2))
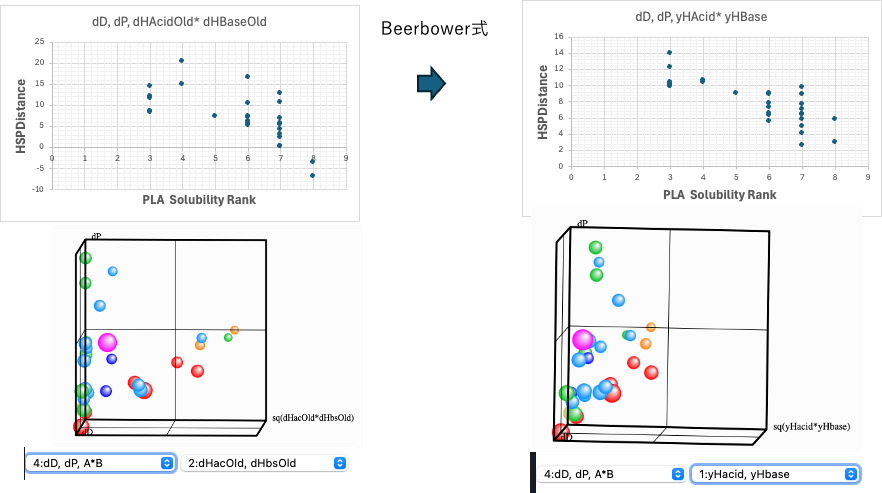
3軸は、dD, dP, A*Bを選び、A, B分割としてdHacidOld, dHbaseOldを選ぶ。dHacidOldがほとんどの溶媒でゼロになるので、dHacidOld*dHbaseOldもゼロになってしまう。そこで溶媒は左の側面に張り付いてしまう。Beerbower距離で考えても山本の分割法は有効である。
CNTの分散性
データは次の論文からとってきた。
Hansen Solubility parameters for single walled carbon nanotube-solvent mixtures
Shane D Bergin, Zhenyu Sun, David Rickard, Philip V Streich, James P Hamilton and Jonathan N Coleman
Journal of Nanoscience and Nanotechnology Vol.8,6082–6092,2008
S. Detriche, G. Zorzini, J.-F. Colomer, A. Fonseca, and J. B. Nagy1
より多くのCNTを分散させる溶媒を良溶媒としてハンセンの溶解球を決定する。
グラフェンやC60と比較してCNTの解析はあまりうまく行かない事を示してきた。
同じ溶解性であってもHSP距離が大きく違う溶媒がある。
ピレンのHSPはYMB26Proで計算した。
CNTではdHをどう分割しても効果はあまりない。
Euclid式での評価
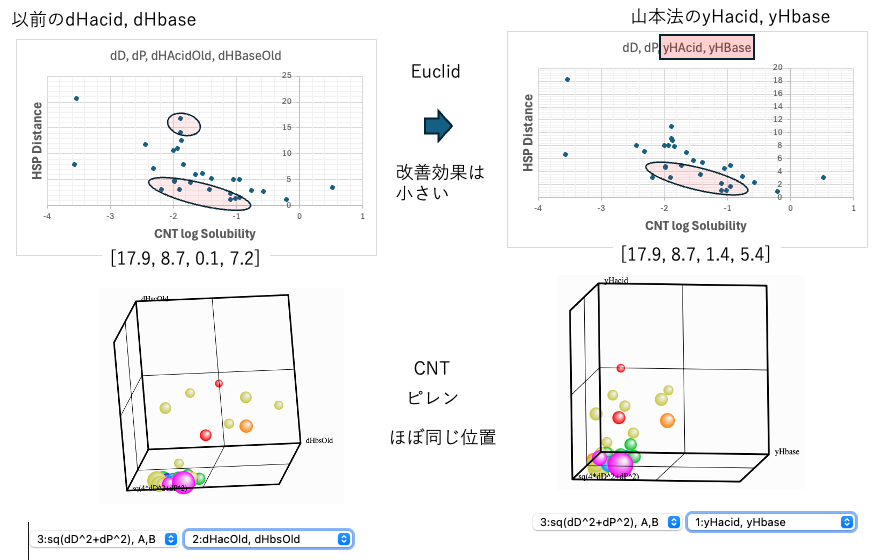
Beerbower式での評価
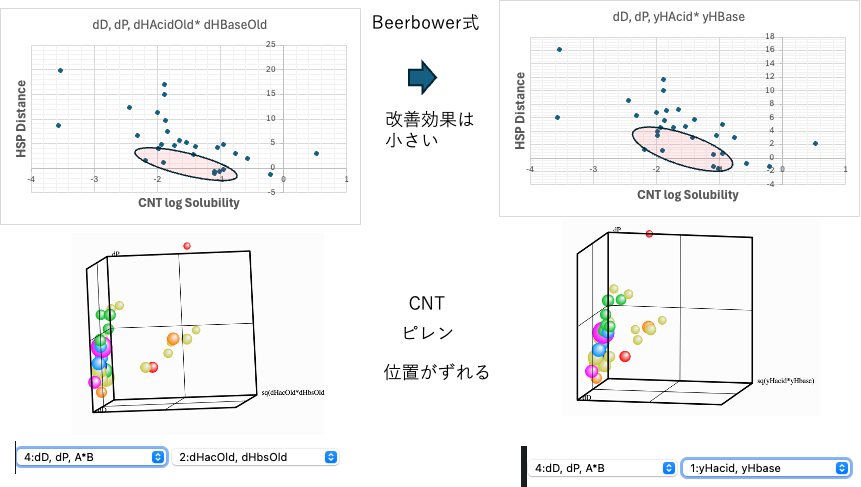
もともとカーボンファミリーのdHは大きくない。それをどう分割してもHSP距離と分散性には大きな相関はない。ところがdHやdHacid/dHbaseを使ったHSP距離と関係なく分散性が変わる現象が厳然としてある。
次世代のHSP2での評価
HSPiPには搭載されていない次世代のHSP2の中にED(Electron Donor), EA(Electron Acceptor)性がある。それが分散性にどう影響しているかは、山本(Pirika.com社CEO)の作成しているPirikaPro4MIの解析例に記載している。
この解析ツールには簡単な分子軌道計算ツールが内蔵されている。先にまずMOで見てみる。
分子を読み込めば直ぐにMO計算される。ここでは多環芳香族としてピレンを計算してみる。
ピレンのHOMOやLUMOはπ電子で覆われている事がわかる。
そして溶媒のHOMOとCNTの分散性にはゆるい相関がある。
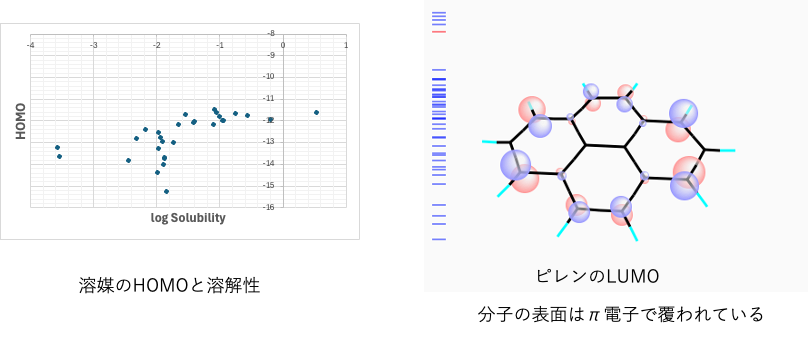
電荷を表示することができる。
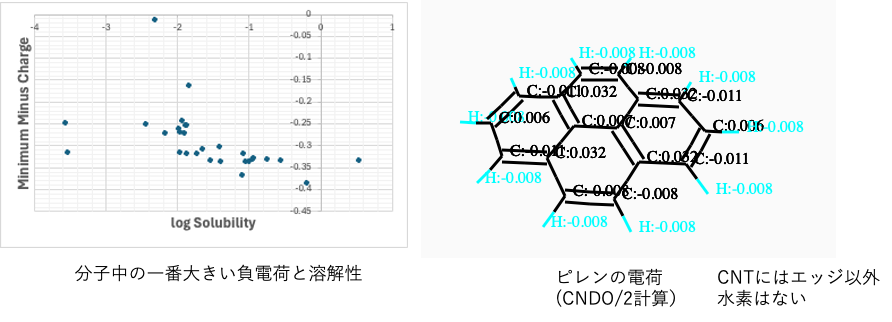
負電荷は小さいほど溶解性は高くなる。
これらの結果から溶媒のローンペアがCNTの分散性に寄与しているようにみえる。
ED, EAを適用してみる。
ED,EAはHSPiPユーザーには関係しないので読み飛ばして欲しい。
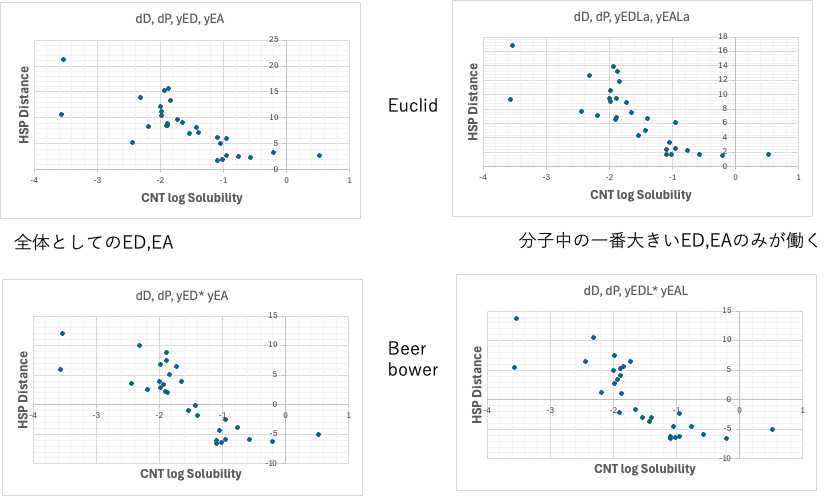
右2つは分子中の官能基で一番大きいED, EA官能基だけがHSP距離に関与したとしての計算になる。ローンペアが分散に寄与しているなら、ローンペアを持つ原子団以外の原子団は分散性には寄与していないと考えられる。
左の２つのモデルは分子全体にED,EAの効果が広がっていると考える。
上の２つのモデルはEuclidタイプの距離の式になる。この場合はHSP距離の最小値はゼロになる。
下の２つのモデルはBeerbowerタイプの距離の式になる。
sign*sqrt((4.0*(dD1-dD2)2+(dP1-dP2)2+2*(yHacid1-yHacid2) *(yHbase1-yHbase2))
2*(yHacid1-yHacid2) *(yHbase1-yHbase2)はacid/baseの値次第でマイナスになりうる。その結果ルートの中がマイナスになった場合には、符号(sign)をsqrtの前に出して距離を計算する。ED/EA, EDL/EALどちらのケースでも大きくマイナスになる溶媒が存在する。
AIによる概要：
カーボンナノチューブ（CNT）の表面は、一般的に電子受容性（EA)であると考えられています。これは、CNTが電子を容易に受け入れる性質を持つことを意味します。ただし、CNTの電子特性は、その構造や化学的な修飾によって変化します。
AIが正しいとすると
距離の式でEDL/EALを使ったBeerbower式（右下のグラフ）が最も近い。
Euclidの式ではED/EA=17.1/5.6 EDL/EAL=16.1/6.3とEDの方が値が大きくなってしまう。
Beerbowerの式ではED/EA=8.3/8.9 EDL/EAL=8.4/9.7となり、少しEAのほうが大きい。
このED/EAをHSPiPに組み込むのは遠い先になるかもしれない。
MIやDXに使う分にはとても有用なパラメータだ。
ニーズ次第でCLI Proバージョンに搭載するかもしれない。
山本法のdH分割
これまでdH分割法はほとんど使われてこなかった。
多くの溶媒ではdHAcidがゼロになるため分割する効果がほとんど無かった。
山本の分割法は多くの系で古い分割法より、より良い結果になった。
EuclidかBeerbowerかで悩ましいが計算をすることによって新しい洞察が得られる。
PirikaPro4MIのユーザーは試してみて欲しい。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください