2022.9.25改訂(2010.2.26)
pirika.comで化学 > 化学全般
> 次世代HSP2, YMB Pro for MI >
> 解析例トップ
その他トップページ > 自己組織化ニューラルネットワーク(SOM)
概要
多次元ベクトルを2次元にマッピングする技術。
似たベクトルは似た位置にマッピングされる。
将来、Sphereプログラムのように、HSPベクトルと付随する情報からマッピングできるように改良が行われている。
内容
HSPのdHをドナー/アクセプターに分割すると、HSPは4次元ベクトルになる。
これは視認性という意味では非常にマイナスだ。
さらに溶解性には分子の大きさが重要なファクターとなっている。
分子の形状を表すOvalityなども、といっているとすぐに5次元、6次元のベクトルになってしまう。
そうした多次元ベクトルを2次元にマッピングする便利な方法がSOM:自己組織化ニューラルネットワークだ。
(JAVAのアプレットを使って実際に計算してみるには、Pirikaのデモ、SOM Appletをお試しください。)
JAVA版は現在提供していません。
JavaScript版のSOMのプログラムはこちらから。
簡易版なので出力などは説明と少し異なる。
SOMについてはこちらも読んでほしい。
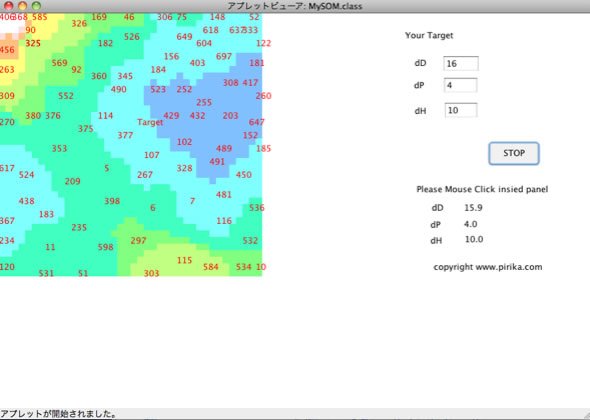
SOMの簡単な原理を説明しよう
SOM: Self Organization Map Neural Network
(N次元のベクトルを2次元にマップする方法)
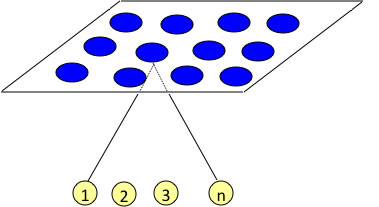
何をしたいかというと、HSPのような多次元ベクトルが溶媒の数だけあったときに、そのベクトルが似ているものは似た2次元位置に配置したい。
3次元までは実際の3次元位置に配置すれば、どれが近いかは簡単にわかる。そこで、ここで扱いたいのは3次元より高い次元のベクトルの場合だ。
例えばm個のベクトルがあったとしよう。
Vec1 [dD1,dP1,dH1,Vol1,…..]
Vec2 [dD2,dP2,dH2,Vol2,…..]
Vec3 [dD3,dP3,dH3,Vol3,…..]
Vecm [dDm,dPm,dHm,Volm,…..]
これらのベクトルを2次元平面に、”似たものは似た位置に”配置したい。

まず最初に、2次元平面に適当なメッシュを切って、その交点にランダムに計算したいものと同じ次元のベクトルを発生させる。

そして、一番目のベクトルを持ってきて、2次元平面上のベクトルが一番似ているものを探す。
その一番似ているベクトルを勝者(Winner)と呼ぶ(下の図で赤いベクトル)。
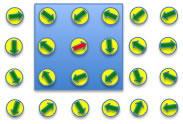
そして、その勝者とその近傍を、ある割合でほんの少しだけ、1番目のベクトルと似た方向へ動かす。
これを1−mのベクトルで繰り返し、さらにそれを何サイクルも繰り返す。
そのうちに収束してきて1−mのベクトルは”似たものは似た位置に”配置される。
通常ベクトルの類似度は、ユークリッド距離を使うが、HSP用のSOMのプログラム中では、dDの前に4が入っている。
化学の場合、こうした、普通の数学とは異なる取り扱いをしなくてはならないので、自分でプログラムを書かなくてはならないことも多い。
簡単なのでチャレンジしよう。
これはHSP距離を計算するときにdDの前にかかる4だ。また、分子体積は平方根を取ったものを使うのが良いようである。
フルバージョンのプログラムでは、表計算ソフトにそのままペーストできるようにテキストベースの出力を持つ。
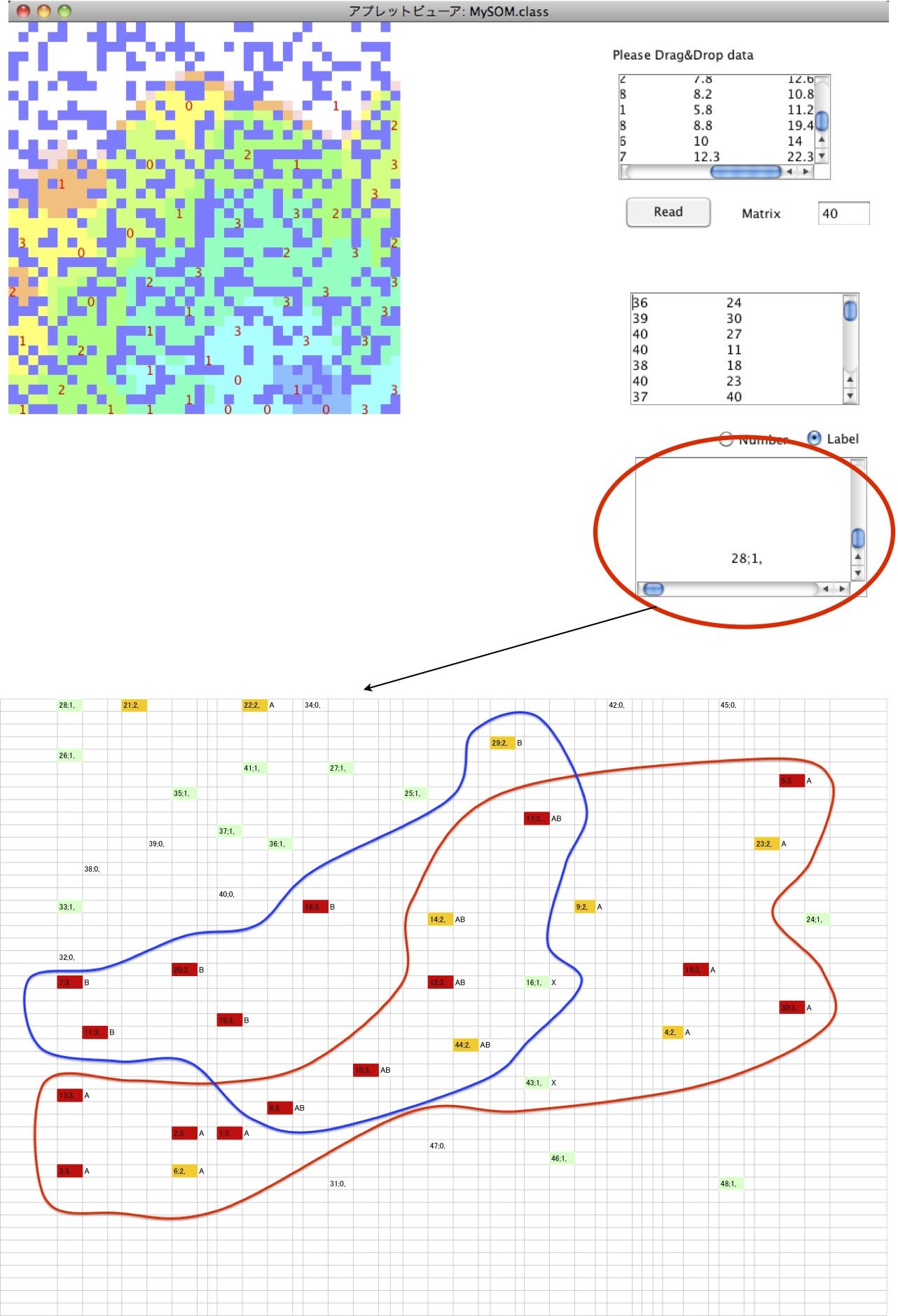
結果を表計算ソフトにペーストし、どのベクトルのそばにどのベクトルがくるか解析することができる。
HSP以外の体積、Ovality、その他の情報からマップが作れるので、非常に有用だ。
pirika.comで化学 > 化学全般
> 次世代HSP2, YMB Pro for MI >
> 解析例トップ
その他トップページ > 自己組織化ニューラルネットワーク(SOM)
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください
