ブログ

隠遁Chemistと愛(AI)の交換日記

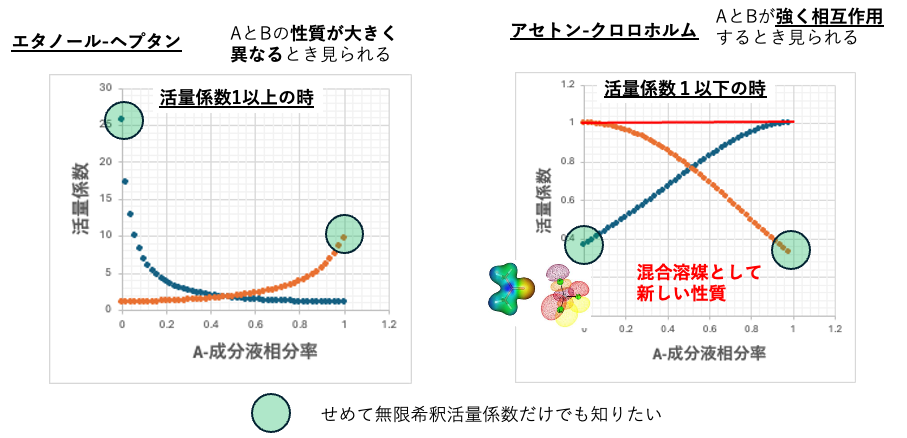
化学工学の分野では気液平衡(VLE)を実測してきた。複数の成分を蒸留して成分分けする必要があったからだ。もし2成分間に相互作用が無いなら話は簡単だ。
混合溶媒は理想溶液として取り扱える。実はハンセンの溶解度パラメータ（HSP)の混合則は理想溶液近似だ。

理想溶液

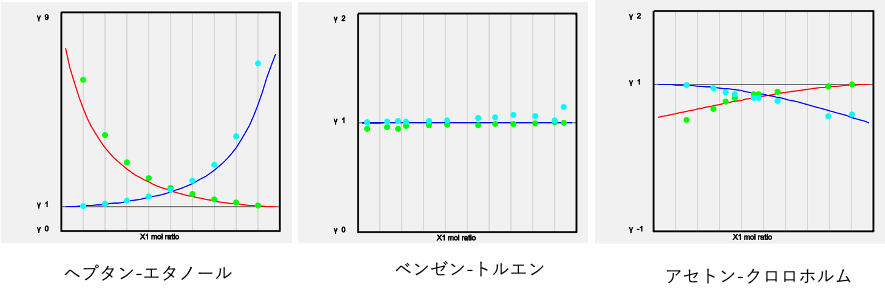
ベンゼンートルエン系

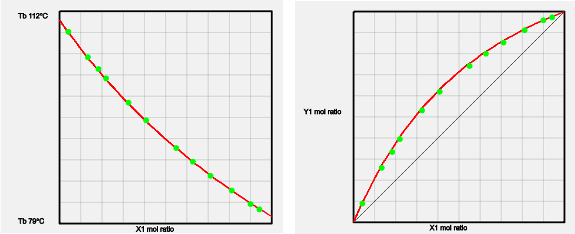
ほとんど同じ構造の分子を混ぜた場合には理想溶液になる。2つの溶媒の比率を変えて沸点や液相と気相の比率を測定する。緑色の小さな点は実測値になる。このような精密な実測値があると、これをパラメータ化してAiSOG法によるVLE推算が可能になる。
AiSOG法の推算値は赤い曲線で示してある。

実在溶液

実際には分子の間には分子間力が働く。もともと同じ分子自体にも分子間力はある。その分子間力を切るエネルギーが蒸発潜熱だ。もし異分子間に反発のエネルギーがあるなら、混合すると蒸発しやすくなる。そこで混合溶媒の沸点は下がる。液相組成と気相組成は大きく異なる。

ヘプタン-エタノール系

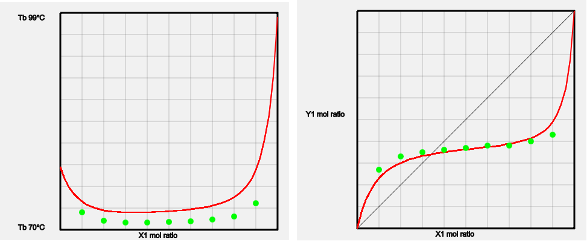
このようなVLEの厳密な測定値（緑色の点）があるのでAiSOGのパラメータを決めることができる。実験値の蒸気圧式(Antoine式のA, B,Cパラメータ）があるなら精度はより高くなる。pirika.com社では分子構造からAntoine式のパラメータを予測する式をHSPiPに提供している。液相組成と気相組成が一致する組成を共沸組成という。共沸の時に沸点が下がる系を最低共沸という。

クロロホルムーアセトン系

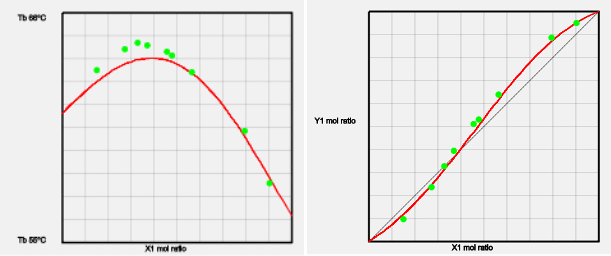
クロロホルム-アセトン強い相互作用がある。そこで混合物の沸点は各々の成分の沸点の足し合わせよりも高くなる。この場合は沸点が高くなるので最高共沸という。

こうした精密な実験値は今後増えるか？

このようなVLEの精密実験は今後どんどん減っていくだろう。各々の純成分を入手して蒸気圧曲線を測定する。その後に組成比率を変えながら平衡組成を測定する。年に何個測定できるだろうか？
それを測定して論文を何個書けるか？

それなら測定など止めてしまおう。誰かが測定した結果をAIを使って解析したという論文のほうがよっぽど効率が良い。

企業はどちらの学生を採用したいだろうか？

次世代HSP

HSPでは無視している実在溶液としての取り扱い。
次世代のHSP²で評価しようとしてきた、マイナスのHSP距離の取り扱い。

こうした研究には2成分を混ぜた時の活量係数の実測値が欠かせない。

でも、今後こうした実測値が増える見込みが無い。

AiSOGで利用できる官能基

AiSOG法は、LLC: pirikacom社CEOの山本博志が作成した気液平衡(vle)推算ソフトウエアーだ。Pirika Pro Add-onソフトに搭載されている。

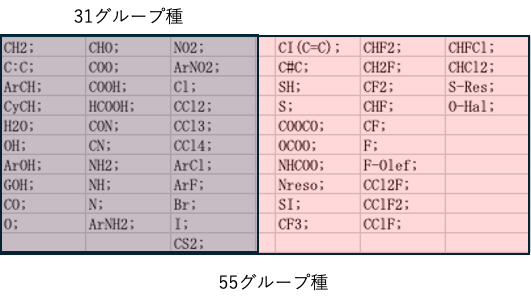
この官能基ペアの局所活量係数を決定しなければならない。

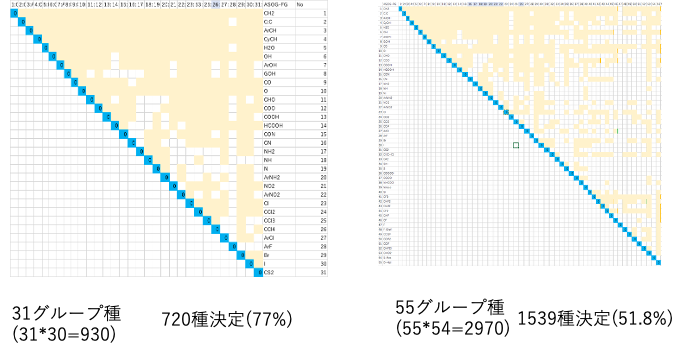
31グループ種(31*30=930)　720種決定(77%)
55グループ種(55*54=2970)　1539種決定(51.8%)

パラメータが決まっていないものはAiSOGで計算できない。
H2N-C(=O)、-HN-C(=O)、>N-C(=O)は区別されないので精度がでない。
区別するように新たに原子団を定義すると、更にきめなくてはならないパラメータが増える。
HSPでは区別している1級、2級、3級アルコールをAiSOGでは区別しない。などパラメータの共用の問題もある。

HSPで使えるが、AiSOGでは使えない官能基もある。

149: P	133: P:O	150: B	153: N=C	154: N=C_R
155: N=N	157: N=CH	158 : N=CH_R	104: OO	169：H-NH3
170: H-H2C=O	172:H-H2O2	52: S=O	119: S=	127: _S{=O}2
107: C(=O)S	134: NO3	152: C=ONHC=O	135: O=	148: N#C

特に硫黄関係のパラメータがないのが大きな問題だ。

HSPを用いたRSMによる活量係数推算

RSM(Regular Solution Model)が適用できるのは正則溶液のみになる。
正則溶液とはTroutoneの通則が成立する（蒸発潜熱を沸点で割った値が一定になる）溶媒と考えてもらえば良い。
Ln γ1= V₁φ²₂(δ₂-δ₁)²/RT
Ln γ2= V₂φ²₁(δ₁-δ₂)²/RT
活量係数が計算できるが、Hildebrandの溶解度パラメータ(δ)の差が0のときに活量係数が1になる。
HSPに拡張したところで、HSP距離の2乗は０以上なので活量係数が１以下を表現できない。
つまり、アセトン-クロロホルムのような強い相互作用を持つものを解析できない。

AiSOG法によるWilson定数推算

ln γ1= -ln(x1+Λ₁₂x2)+x2(Λ₁₂ / (x1+Λ₁₂ x2) – Λ₂₁ / (Λ₂₁x1 + x2))
ln γ2= -ln(Λ₂₁x1+x2) – x1(Λ₁₂ / (x1+Λ₁₂ x2) – Λ₂₁ / (Λ₂₁x1 + x2))

Wilson定数、Λ₁₂、Λ₂₁を決めるには高精度な実験が必要だがそれが増える見込みが無いことは説明した。

HSP-AiSOG法

今後、実測値が増えない事を前提に、今可能な限りの拡張を行っておく。
ハードディスクの肥溜めを探したところ、無限希釈活量係数の一覧が出てきた。
様々なソース、化工便覧とか書籍から色々集めた。
トータルで7,157溶媒ペアの無限希釈活量係数のデータがあった。
こうしたものを今集めようとしても不可能だと思う。
どこも情報を出さなくなった。情報はどんどん希釈され、検索しようにも出てこない時代になった。
そこで今のうちに、RSMとASOGを結びつける技術を完成させてしまうことにした。

Margules Parameter, 無限希釈活量係数

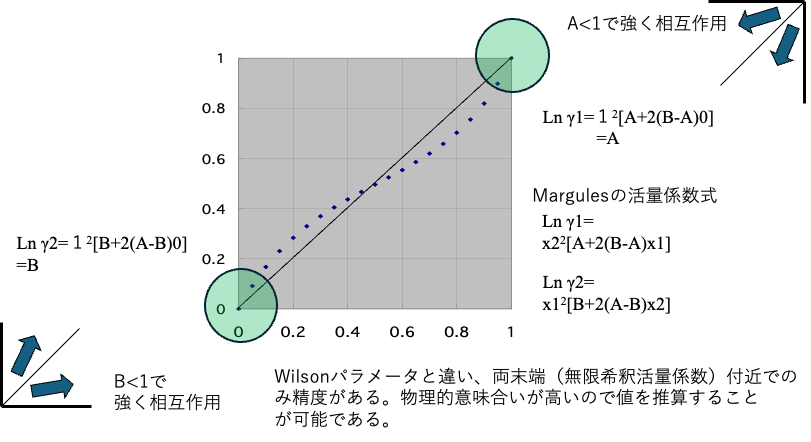
Margules式は次のように表すことができる。
Ln γ1=x2^2[A+2(B-A)x1]
Ln γ2=x1^2[B+2(A-B)x2]
両末端（無限希釈活量係数）では、Ln γ1=A、Ln γ2=Bになる。
A<1、B<1で溶媒同志が強く相互作用してしていることがわかる。

Ln γ1= A = -ln(Λ₁₂)+1 – Λ₂₁ =V₁φ²₂(δ₂-δ₁)²/RT

Margules式はWilson, RSMを結びつけることができる。

拡張RSMの開発

RSMでは活量係数が1以下にならない。それを解決する。
今回発掘した無限希釈活量係数と3D-HSP²をプロットしてみる。

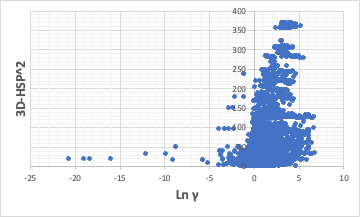
3D-HSP距離²は、(δD1-δD2)² + (δP1-δP2)² + (δH1-δH2)² +となる。
3D-HSP距離²が大きくなるとLnγは大きくなる傾向がある。
溶媒が強く相互作用するにはLnγが0未満になるが3D-HSP距離²は常に0以上なので表現できない。
そこでLnγが0未満を表現できる式を様々検討した。

ルイスの酸塩基交換作用

結論から言えば、ルイスの酸塩基交換作用がLn γをマイナスにしている事がわかった。

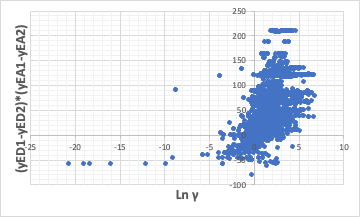
次世代のHSP²の33式で検討したが、山本が定義したElectron Donor/Acceptorの交換項がLn γをマイナスにしていることがわかった。
(yED1-yED2)*(yEA1-yEA2)
弱酸と弱塩基の塩に強酸を入れると交換反応が起こるのと同じだ。

このHSP距離がマイナスになる距離の式と分子のサイズや球形度を加味したLn γの予測式をニューラル・ネットワーク法を用いて作成した。

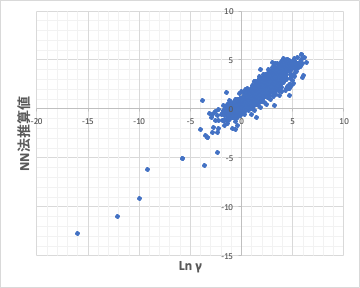
この精度で十分かというと議論の余地はある。

AiSOGで計算できるものは計算して比較してみた。

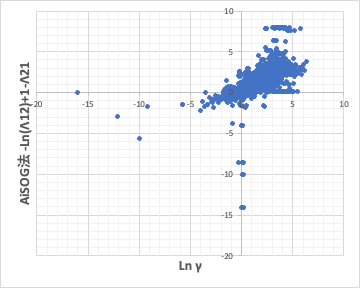
Ln γ1= A = -ln(Λ₁₂)+1 – Λ₂₁ の関係があるのでプロットしてみると上図ぐらいの精度になる。H2N-C(=O)、-HN-C(=O)、>N-C(=O)は区別されないので精度がでない。-5以下の化合物はアミドの形式が異なるもので、これに関してはNN法の方が精度がたかくなる。

HSPが計算できる化合物であれば活量係数を評価できるようになった。

HSP距離が長いのに溶解する
HSP距離が短いのに溶解しない

これまで例外とされた溶解性に活量係数を導入することが可能になった。

Pirika Proに搭載した！
ユーザからのフィードバックが楽しみだ。