2025.06.10
pirika.comで化学 > 化学全般
> 次世代HSP2, YMB Pro for MI > HSP2に後光がさしている
> ハンセン溶解度パラメータ (HSP) Doc
注意：HSPiPの機能ではありません
堀場とAshizawa共催の粒子分散評価セミナー2025に行ってきた。
英弘精機さんの発表で、後方散乱の話があった。僕は2023年のドイツであった、HSP-specialist workshop at UDEに招待された。そこでオランダのVLCIが微粒子のHSPを自然沈降法で測定していた。彼らはHSP50周年記念講演会の時からの知り合いだ。
今回のスタビリティーテスター(ST-1)の測定法は彼らのものと似ている。今回説明するFinnTalcM15のLumisizerでの測定に関しては「微粒子のハンモック、δNet : 分散に対する新しい指標」で解説している。ここでは微粒子と分散安定剤あたりも含めて説明する。
もとの考え方はこちらを参照してほしい。
Using-HSP-to-Improve-the-Dispersibility-of-Pigments-and-Fillers.pdf
沈降時間と相対沈降時間のデータ
VLCIはデータを公開していないから、Lumisizerのデータを流用した。
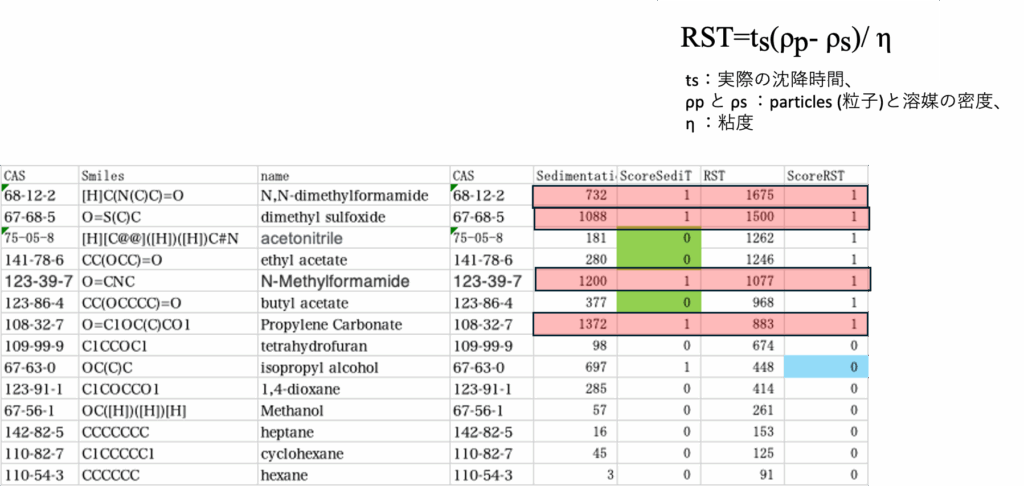
分散安定性を沈降時間で見るか、相対沈降時間(RST)で見るか？
実はHSPiPではRSTで見ることを推奨している。
僕は余りRSTを信用していない。
もう少し大きな粒子ならストークスの理論も良いかもしれないが、ナノ粒子ぐらいになると当てはまらない事も多くなる。
結局は両方やって良い方を取るしか無いと思っている。
沈降時間を使って溶媒のScoreを決める
まず溶媒のScoreを決めなくてはならない。良溶媒をScore=1, 貧溶媒を Score=0に設定する。詳しいことは「初心者のためのHSP」を読んでほしい。いきなり例えば沈降時間がXXX以上をScore=1とか設定している論文がある。でも、まずはデータをよく見てみよう。
マウスでドラッグすると回転する（Shift-Drag:拡大縮小、Option-Drag:移動）
球をクリックすると溶媒名が表示される。Score=1と設定した溶媒は青色の球、Score=0と設定した溶媒は赤色の球で示してある。
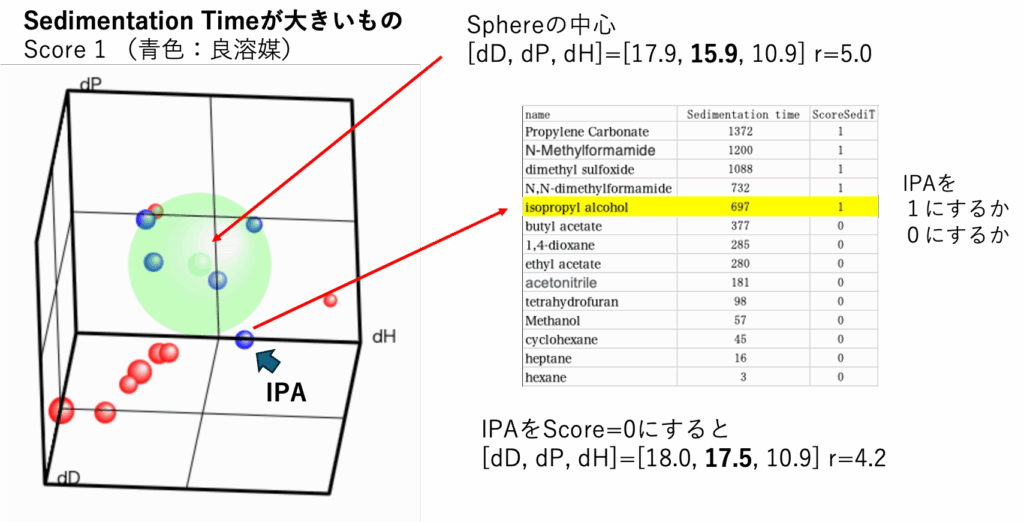
ハンセン先生の理論では、良溶媒がハンセン空間に集まっていると考える。
しかし、IPAをScore=1にしてしまうと、IPAはハンセンの溶解球に入らない、Wrong Outになってしまう。
なぜそうなるのか、ちゃんと理解しておこう。IPAをハンセン溶解球の内側に入れるほど半径を大きくすると、今度はScore=0とした２以上の赤い溶媒が溶解球に入ってしまう。
できることはIPAをScore=0にするだけだ。
すると求まる溶解球の中心はdPが少し大きくなる。このようにScoreの値を変えると求まる溶解球の中心は変わる。HSPは沸点のように１つの物性値に決まるものでは無いことを覚えておこう。
RSTを使って溶媒のScoreを決める
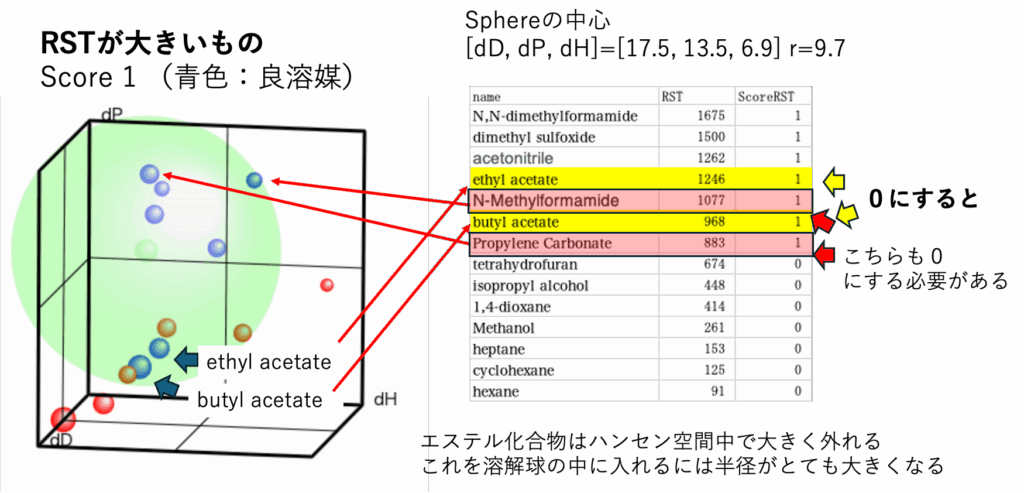
RSTを使ってScoreを決めるのは実はものすごく難しい。でも、論文とかできちんと触れているものは見かけない。
エステル化合物はハンセン空間でとても離れた所にいる。溶解球を探索すると、とても大きいは半径になる。２つを外すよりも、大きな溶解球を使って、間違って溶解球に入ってしまうWrong Inが1,4-Dioxaneだけの方が良いモデルと判断してしまう。そこでどうしても研究者の関与が必要になる。
しかしエステルを外す(Score=0にする)と、RSTの大小で言えばN-MethylformamideとPropylene Carbonateも外さなくてはならなくなる。
良溶媒は３つしか無くなってしまう。
Wrong In/Outが少ないモデルが良いモデルかどうか？はよく考える必要がある。（論文に書くときは見栄えが良いが）
安定性の高い、微粒子が沈殿しない溶媒を探索して特許を取りたいなら、容易類推できない溶媒探索をしたい。目的次第だろう。目的を持てないAIの苦手な分野だ。
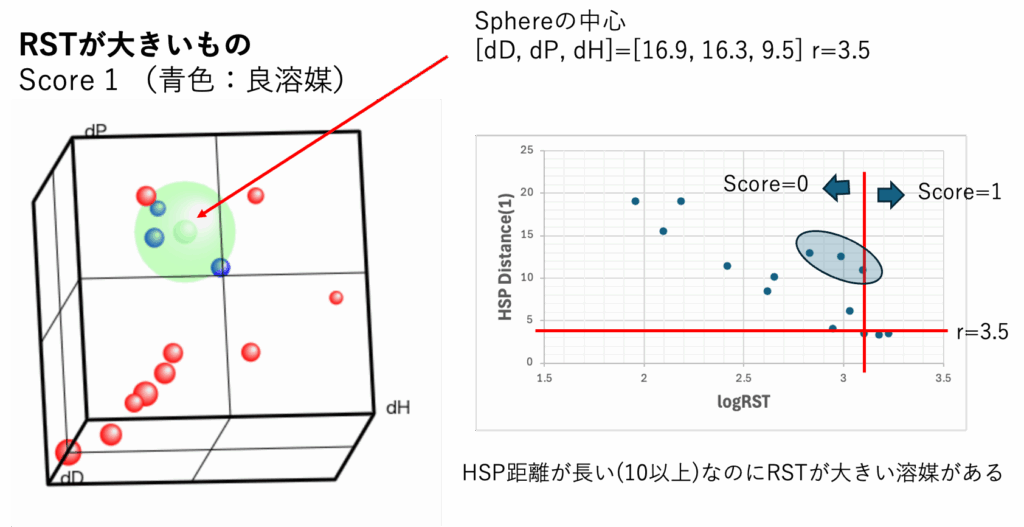
HSP距離が短い溶媒を探索したいが、HSP距離が長くても大きいRSTの溶媒が存在する。あまり良いモデルとは思えない。
Double Sphereがあるとすると仮定したくなる
HSPiPソフトウエアーに搭載されているDouble Sphere法は、例えばブロックコポリマーの溶解性のように、異なる溶解部分があると仮定して、溶解球を２つ探索する。
この探索ルーチンは僕が作ったくせに自分では安易に使わないようにしている。
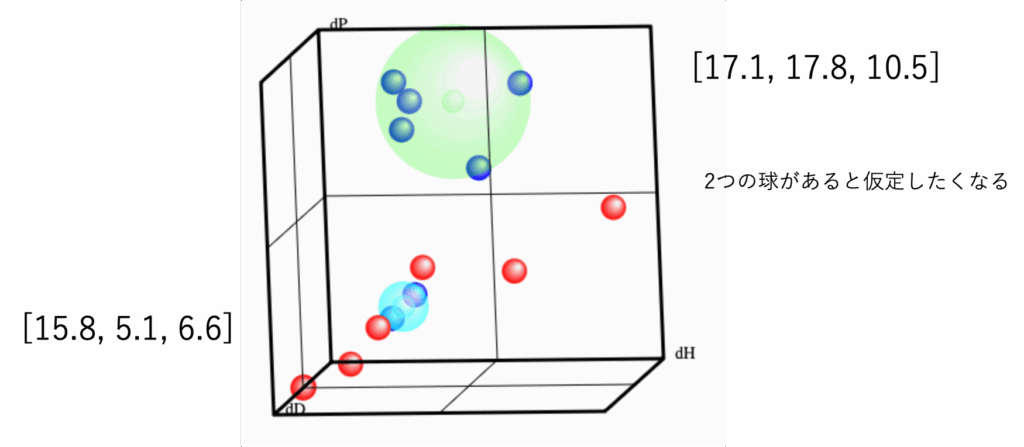
実際には無機物の表面に二つの表面があることはあり得る。
Score0,1の取り方によって求まるターゲットのHSPは皆異なる
これは挟み撃ち法の限界だ。「あなたは、酸？ 塩基？挟み撃ち法の限界？」で解説した。
挟み撃ち法で決定できる事自体はとても良いことだ。MOやMDで材料設計するのと比べて、中身がブラックボックスでも良い。しかし、純粋なブレンステッドの酸が無い（カルボン酸などは両性）と挟み打てない。
挟んだものだけからHSPが決定されてしまう。
実数をScoreにとる
HSPiPにもData Pointsという実数をScoreに使う方法が搭載されている。この機能も僕が作ったものが搭載されている。この機能はHSP距離と実数が一番高い相関になるような溶解球の中心を求める。
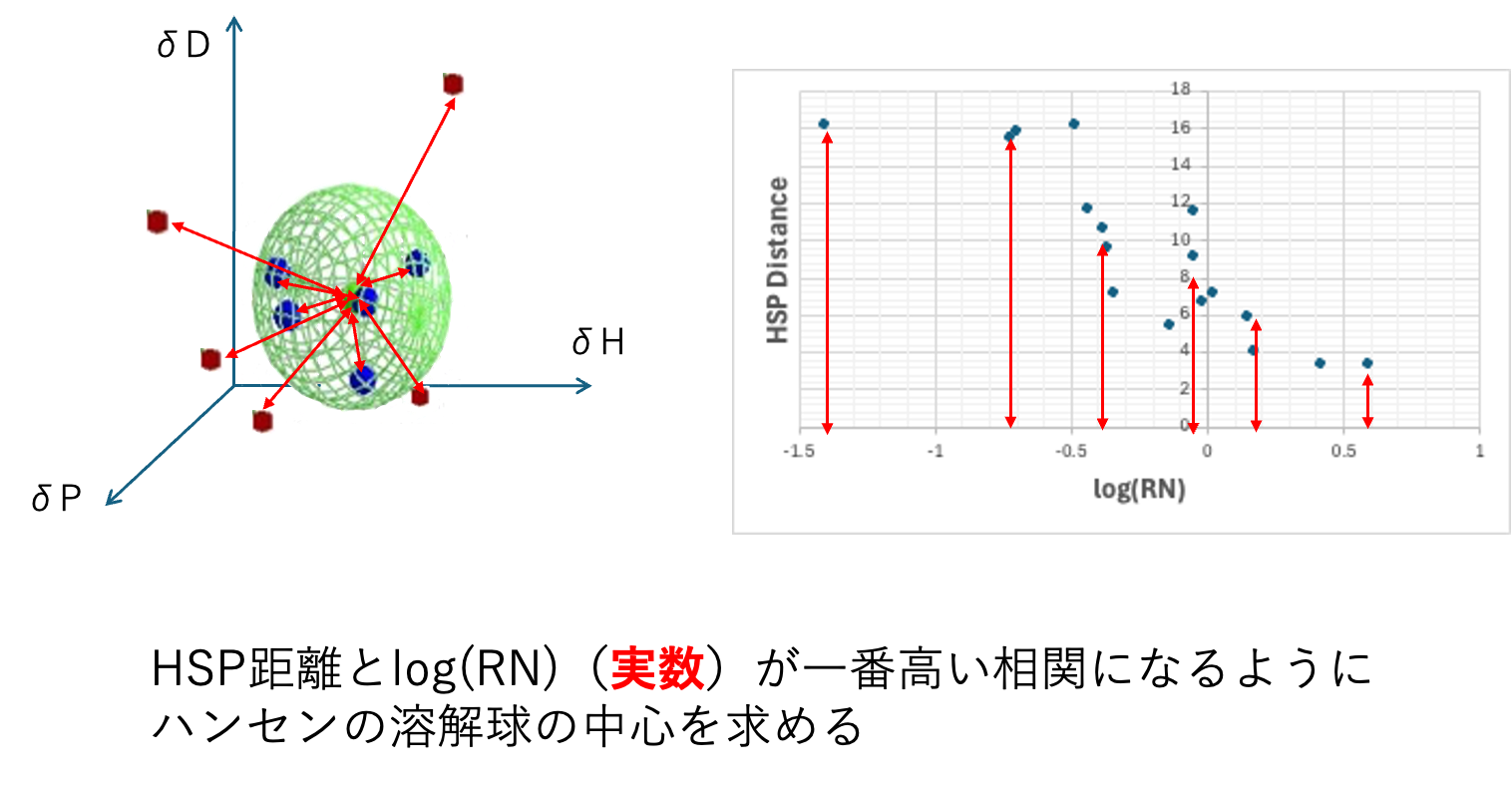
単に相関係数だけを見ている。相関係数は１つでも悪いものが入ると相関係数をとても悪くする。きちんとグラフで見ていく必要がある。
log(沈降時間)を実数
ここでは、青い色ほどScoreが大きい。赤いほどScoreが小さくなるように溶媒に色をつけている。まだ軸の選定は行わないでぐるぐる回してみてほしい。
log(RST)を実数
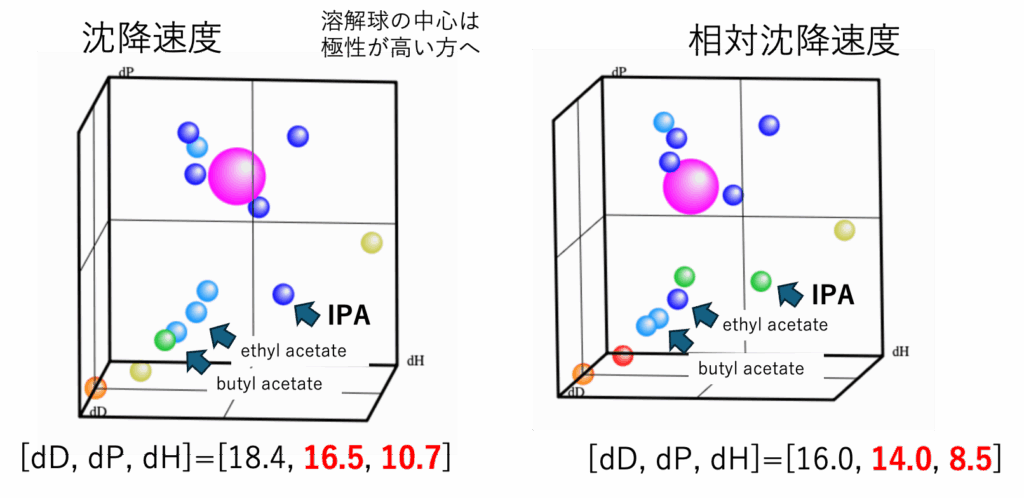
マゼンタの大きな球が溶解球になる。0,1の境界があるわけでは無いので、溶解球の半径は意味がなくなる。
溶媒のHSPは変わらないので3次元の溶媒位置はどちらのプロットでも同じになる。
溶媒の色は沈降速度で見た時とRSTで見た時で異なる。こうして求まった溶解球の中心からのHSP距離と実数が一番高い相関になる。
HSP距離と実数の相関
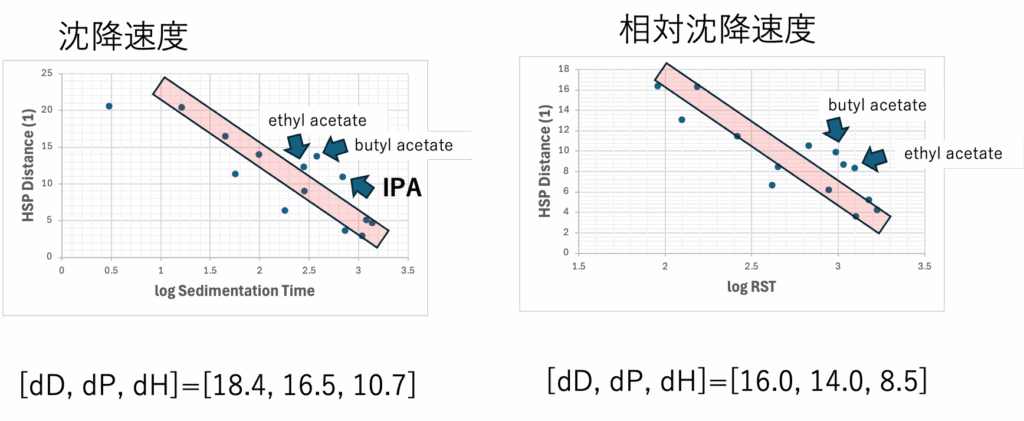
沈降時間の時のHSP距離=sqrt(4.0*(18.4-dD2)2+(16.5-dP2)2+(10.7-dH2)2)
RSTの時のHSP距離＝sqrt(4.0*(16.0-dD2)2+(14.0-dP2)2+(8.5-dH2)2)
RSTの時に求まる溶解球の中心が極性が低い方へシフトする。
それは、エステル化合物が極性が低いのにRSTが高いために起こる。挟み撃ちが反映されてしまう。
微粒子のハンモック、δNet : 分散に対する新しい指標で詳しいことを記載しているので確認してほしい。
軸を[dD, yED, yEA]軸に変えてみよう
セレクターで[dD, A, B]を選んで、dHの分割をyED,yEAにしてプロットしてみよう。
距離の式としては7式を使う。
沈降時間でのHSP距離=sqrt(4.0*(18.6-dD2)2+(17.1-dP2)2+(4.2-yED2)2+(3.4-yEA2)2)
RSTの時のHSP距離=sqrt(4.0*(17.2-dD2)2+(14.1-dP2)2+(3.5-yED2)2+(2.3-yEA2)2)
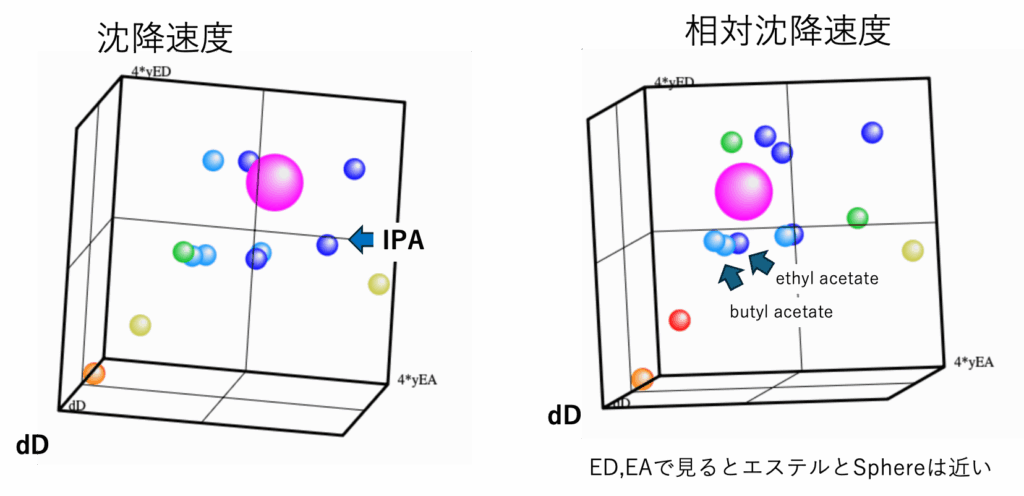
[dP, yED, yEA]軸にしてみる
軸には3つしか選べないので、何枚かに分けなくてはならない。そこがわかりにくい。
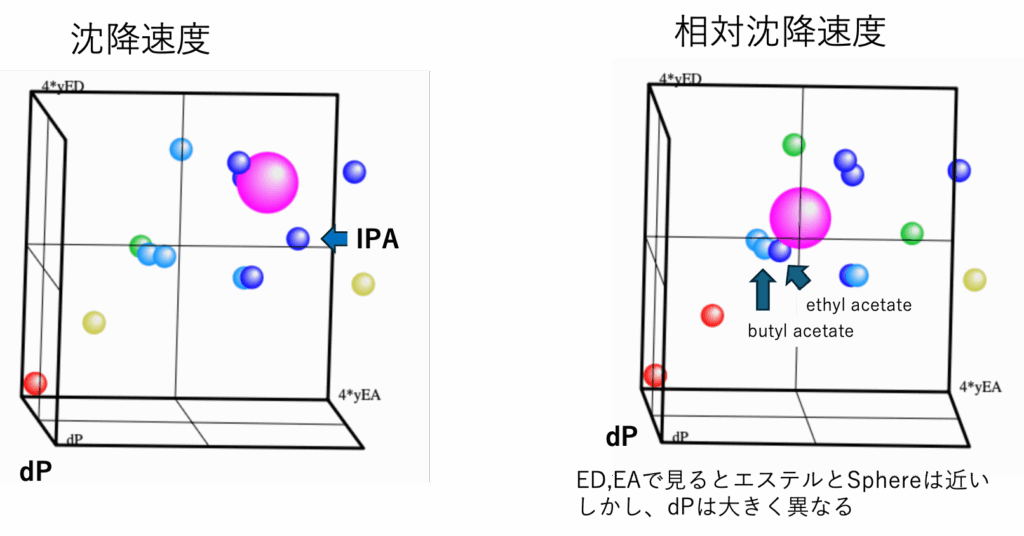
RSTの場合エステル類のED,EAは溶解球とかなり近いように見える。
しかし回転してみると溶解球とエステル類のdPの値はとても離れていることが分かる。
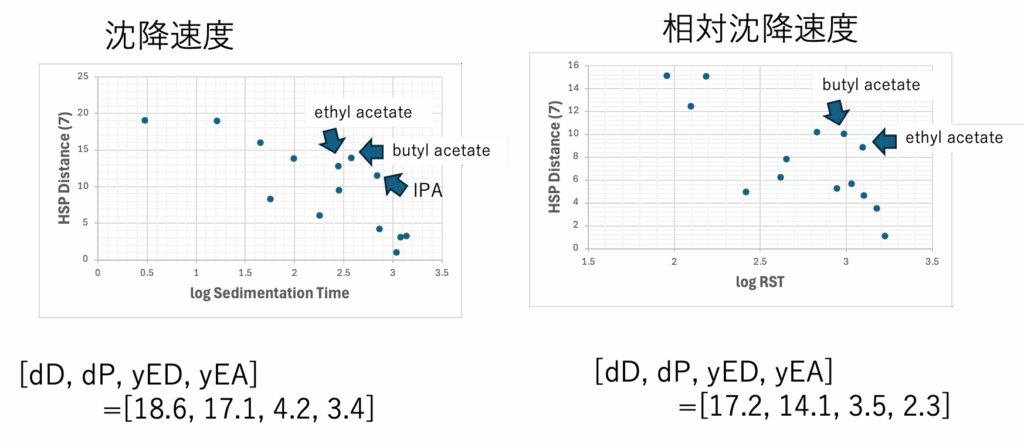
そこで、RSTで求めた(7)式ではエステル化合物の距離はどうしても長くなってしまう。
沈降時間と単相関の高い物性値
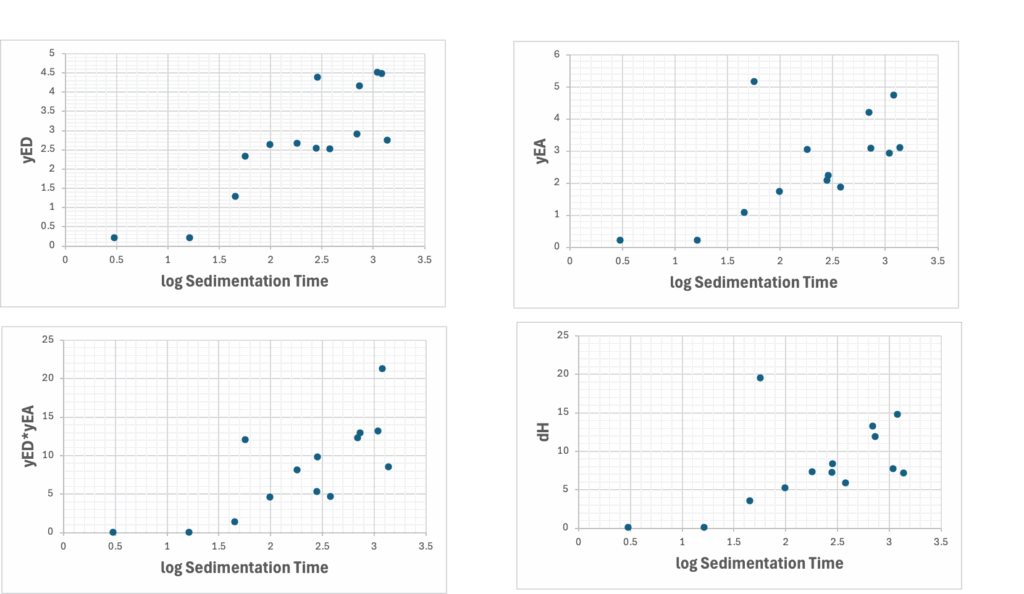
沈降時間はEDやEAととても高い相関を持っている。また溶媒のdHだけとも高い相関がある。dP項を取り除いた3次元HSPでも十分な性能になるだろう。
RSTとの単相関
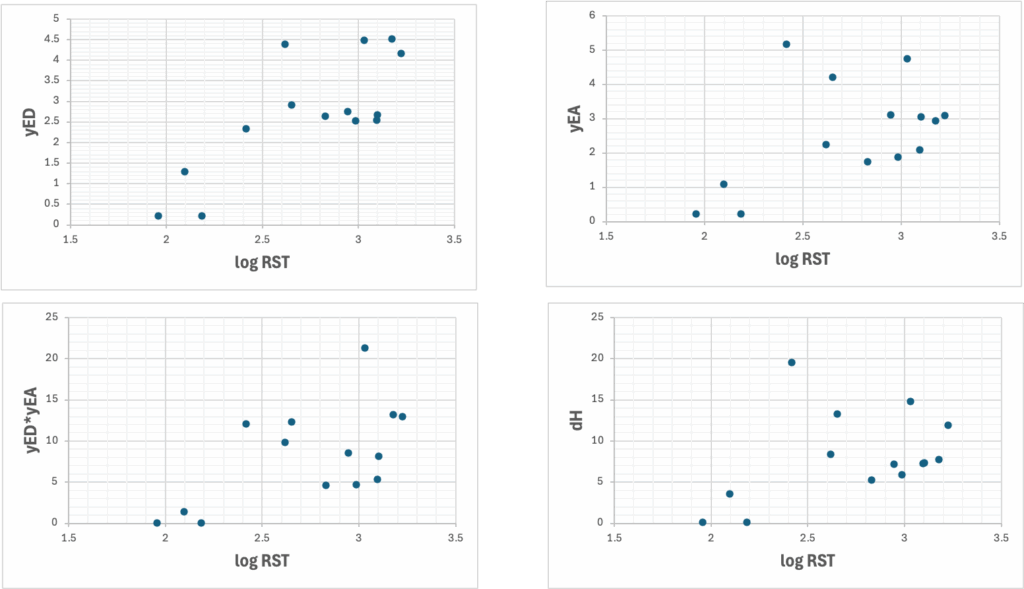
ところがRSTにしてしまうと、EAやdHの値との相関がとても低下してしまう。
そこでEDやEAを使った新しい距離の式を導入しても効果が低かった。
なぜRSTにするとEAやｄHとの相関がなくなるか？
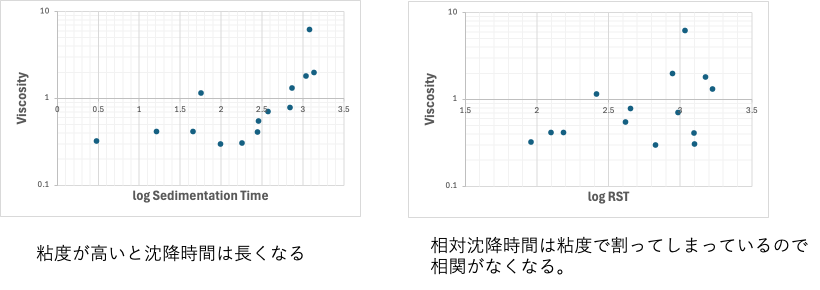
沈降時間は粘度の高いものほど長くなる。それはいいだろう。
RSTは粘度の補正を入れているので、粘度との相関は低くなる。
粘度はどんな物性に基づくか？
分子が大きいものは粘度が高くなる。
水素結合のようなネットワークを作るものは粘度が高くなる。
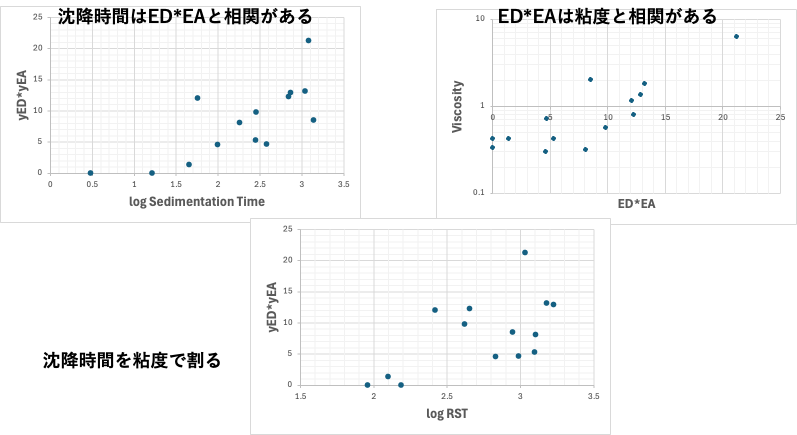
RSTの大きな溶媒を探索しようとすると、粘度の低い、ED*EAの小さな、小さい分子を探索してしまう。dNetのハンモックのような溶媒探索はできない。
ED/EAの前につく”y” はYamamotoのy
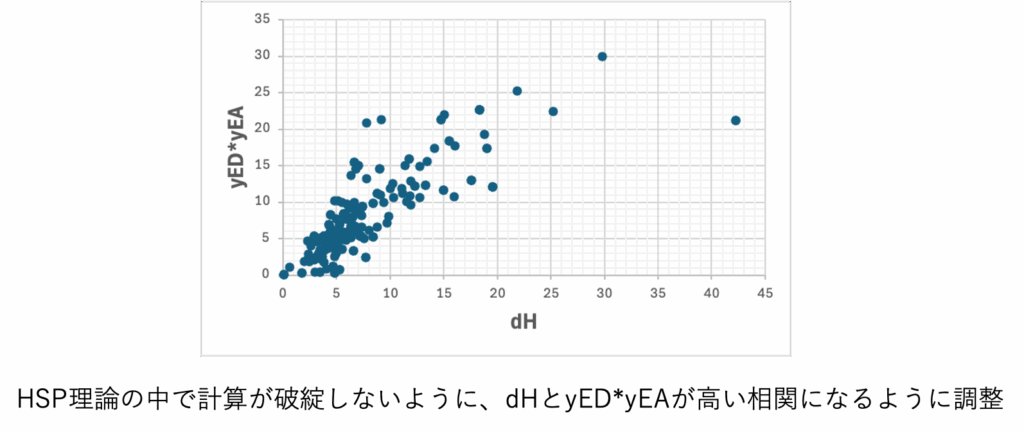
HSP理論は1967年の発表以来輝き続けている理論だ。そこに変なものを持ち込んでも返って悪くなる。僕はHansen先生達と仕事を始めた2008年以来、長いことチャレンジしては打ち返されてきた。やっと見えてきた一つの解がこのパラメータだ。HSP理論の中にも取り込めるようになった。
GutmannのDN/AN
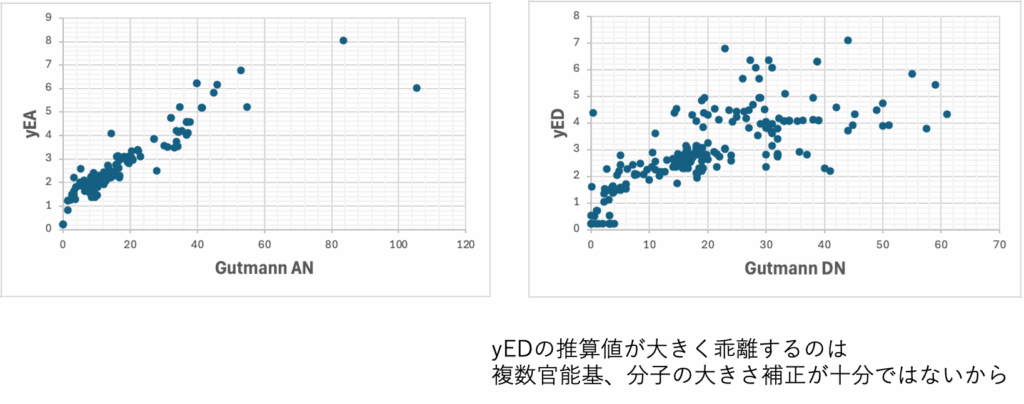
YMBProはSMILESの構造式からyED, yEAを推算することができる。GutmannのANとの相関は高いが、DNとの相関は少し低い。これは複数官能基を持つ化合物や分子の大きさの補正が十分では無いからである。もともとGutmannのDNは中和熱、ANはりんのケミカルシフトなので、2つを掛けたものの単位はあって無いようなものだ。それをほかの蒸発潜熱にもとづくHSP、dDやdPの式に直接いれては計算が破綻してしまう。
2017年のHSP50周年の時に既に発表しておきながら、使いこなせるように8年も要してしまった。
分散安定剤
VLCIのHPの記載では、微粒子にさらに分散安定剤を入れて評価している。
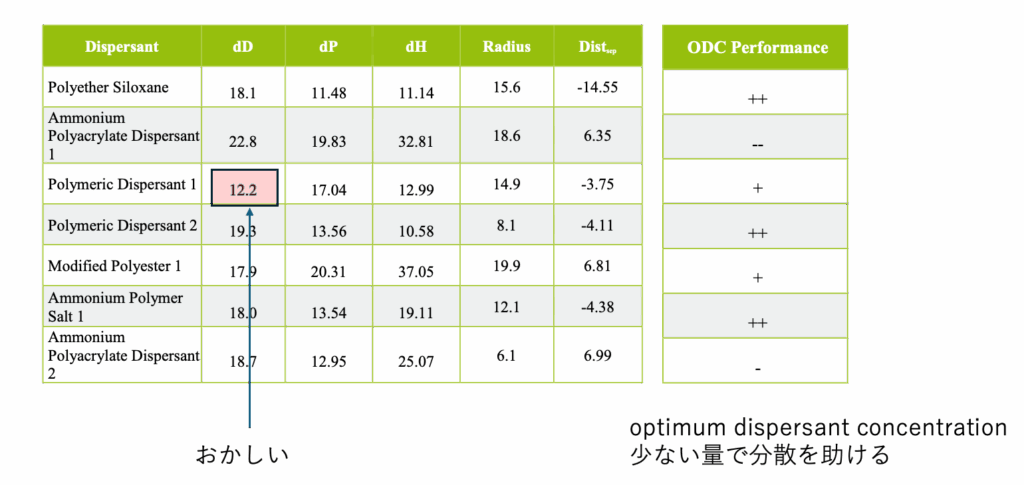
7種類の分散安定剤を溶解性試験を行いHSPを求めている。
残念ながら溶解性試験のデータはオープンになっていないので計算し直すことはできなかった。評価は添加剤を加えた時にどれだけ粘度が下がるか、どれだけ少ない添加量で安定化できるかが評価されている。
微粒子＋安定剤＋溶媒のシステム設計
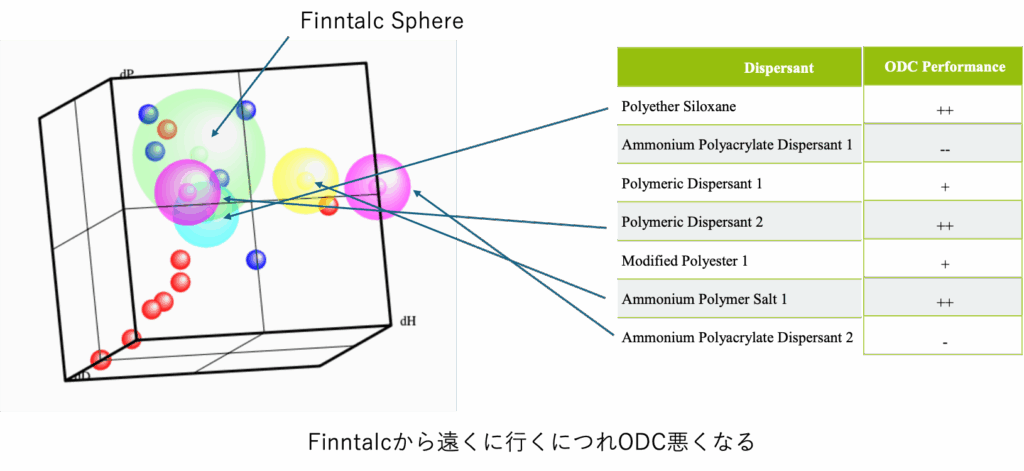
FinntalcのSphereはここで計算したものを使い、資料に書いてあった安定剤のHSPを一緒にプロットした。Finntalcに近い安定剤が++評価を受けることが確認される。ここまではHSPiPを使っても評価できる。
それでは、今回分かった「yEDやyEAが重要だ」という事を、昔の[dD, dP, dH]しかないデータに適用するか？ だ。
とてもざっくりだが、次の関係を使う。
dH=yED*yEA
とりあえず、yED=yEA=sqrt(dH)としてしまう。結果に後光が差していたら溶解データから見直す。
インクや触媒インクなどを設計する時には、このあたりのマッチングが大事になる。
SF Box理論などに上手に適用できればと思う。
セミナーでは温度履歴による凝集状態の変化なども紹介された。
HSP的には温度の違いは鬼門だ。
こうしたデータがもっと増えてくれると更に色々な解析が進むだろう。
データが一杯公開されることを望んでいる。
後光が眩しくて見えない？
RSTの理論は大先生が提唱している理論だ。御威光に逆らってはいけない。
でも、みんなが眩しがってひれ伏している隙に特許を押さえるのは企業では大事だ。
全部が理論通りなら、すぐにAIがみな特許を取ってしまうだろう。
どうも、そんなつまらない時代にはまだならないと感じさせてくれるセミナーだった。
そんな事を考えるようなセミナーを企画してくださった堀場さんに感謝！
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。